Was an adjustable simulator used according to para. 4.5.2 (f)? Check.
Was the feature contained by a simulator of "perfect" form and inverse shape of the specified geometry per the irregular FOS definition? Check.
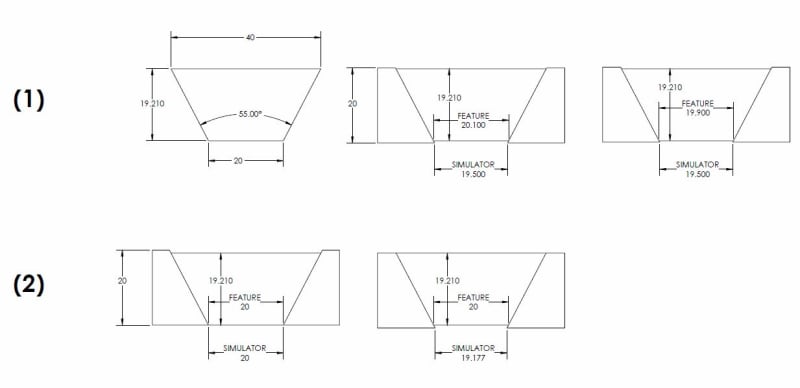
If you're asserting that this is a valid example of a UAME for an IFOSb then you've left out the fact that such an envelope must be of largest (internal feature) or smallest (external feature) size. Regardless of whether size is defined for a conical feature, largest/smallest requires at the very least a maximum/minimum limit - where is this maximum/minimum limit for a conical primary datum feature simulator which results in identical simulation now matter how much adjustment is made to the "size" ?
A single planar primary datum feature can be simulated by a movable simulator as well, it doesn't mean that movement or offset is in any way relevant to the simulation process.
I fully agree. That is also why I am against the "unlimited offset" argument.
You're going to have to explain to me how these two statements jive. You agree that offset (and I hope from our conversation thus far you realize by offset I meant all analogous behavior for a conical simulator ie: axial movement and contraction/expansion) is not necessarily relevant to the simulation process for a conical feature but still say that an offsetting simulator for a conical feature is an example of valid "second type of behavior" ?
but can you simulate a truncated cone with it? No. Because it doesn't work without the physical joint representing the apex.
A simulator for a truncated cone does not have to be a truncated cone. A fully formed cone as well as a truncated cone would result in equivalent simulation of a conical primary datum feature, I'm not clear on why you believe otherwise.
If you're saying that a fully formed cone doesn't mimic the behavior of a truncated cone, it doesn't matter if this apex is physical or theoretical - such an intersection can be derived and the behavior is the same.
With this specific physical mechanism example, you portray the apex point as a crucial feature that it really isn't. The apex point is defined by and dependent on the characteristics of a given conical surface (base size and included angle), but not vice versa - i.e, the conical surface doesn't depend on the existence of an apex. The only mandatory theoretical geometry outside of the surface outline needed to fully define a cone is the axis.[
It certainly does. A truncated cone has no physical axis or vertex - these are both theoretical geometry existing within or without the material, the fact that you can't see or touch them does not matter. I only utilized a physical example of a joint to provide something physical to better imagine my point. In a truncated cone this vertex is theoretical but an intersection still exists. In both cases the axis is fully theoretical but you clearly have no trouble acknowledging such an axis exists, why you can't apply the same logic to the apex is mystifying.
In that sense, a cylinder can be viewed as a special case of a cone with 0° slope (I'm aware that this is not entirely "by the book")
I'm sorry, I'm going to have to strongly disagree with this - even though as you can tell I'm a supporter of creative interpretations. Switching the convention** to slope of the line segments (half the included angle) does not change the requirement that the shape must have a vertex/intersection point which at which the line segments meet to create the included angle. Two parallel, non-intersecting line segments such as would be found on a cylindrical feature do not have an vertex/intersection point by any definition and therefore no included angle which is the basic requirement for a cone no matter how far I might stretch the definition.
Below is a simplistic version of what I mean. A through D have included angles and intersection points - A being 180 degrees, D being 0 degrees, and C/D being somewhere in between. E has no intersection and does not have an included angle. While not something I have an issue with personally, I understand the difficulty in discussing cones or intersection points with 0 or 180 degree included angles - but to suddenly make the leap to a cylinder (E) where there is not even the possibility of an intersection point to me follows neither logically nor geometrically.
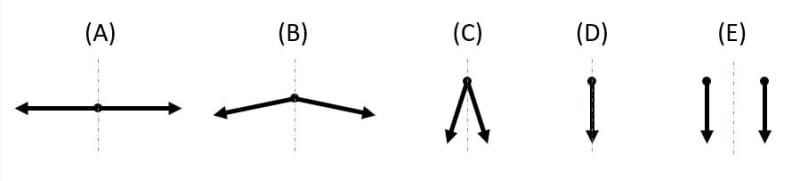
A cylinder of any nonzero diameter is not a cone in any sense or "special case". The only thing I will concede is that a cone of 0 degree included angle is a line which MAYBE one could say is a cylinder with a diameter of zero, but I don't see much use in discussing cylinders having no diameter especially as this logic does not apply to any other cylinder for as soon it has any nonzero diameter it is absolutely not a cone (no intersection/included angle). Though if I'm to go by your previous statements if you do have issues equating a 180 degree included angle cone with a plane I would think you have the same issues equating a 0 degree included angle cone with a line - the fact that you would make the leap from a 0 degree cone to a cylinder of any diameter seems incongruent (though as I said equating it to anything other than a cylinder of zero diameter is not supported by the geometry involved).
If the slope angle is changed to 90° (180° included angle) then the axis becomes of zero length; the only meaningful length of any axis of a theoretically perfect feature is the portion at which it connects center points of cross-sections of the theoretical surface which it is related to. This effectively eliminates the existence of a surface of revolution - there is nothing to revolve around, therefore the resulting geometry is undefined as a surface of revolution. If it is no longer a surface of revolution then there is certainly no equivalence with a cone.
What I personally believe is that the axis is really of infinite length - as long as it bisects the angle theres no reason to limit it to the length of the feature. So a planar feature could have an axis consisting of any line normal to the surface. But perhaps thats a bit of a stretch for most people. Your statement that there is "nothing to revolve around" could be countered with the existence of such an infinite axis, or even without it I see no reason that anything existing in the same plane could be revolved around a single point instead of an axis. Do you not agree that a point could be revolved around another point to create a circle? Same concept.
Setting all that aside for the moment, can we agree that geometrically there exist features of 0 degrees included angle, 180 degrees included angle, and everything in-between? Going by stricter definitions a cone is the set of possible features having an included angle between 0 and 180 degrees, bounded on one end by a shape having included 0 degree angle which is a line (or a cylinder with a diameter of zero) and on the other end by a shape having included 180 degree angle which is a plane.
Nowhere within that set (between 0-180 degrees) or the bounds (0 and 180 degrees exactly) exists a cylinder of any NONzero diameter which is why I disagree with geometrically equating a cone and cylinder of nonzero diameter. Conversely, one of those bounds (180 degrees) is a plane which is why I have asserted the similarities between a cone and plane.
**Edit - I see you may be referring to the calculation for (D-d)/L you mentioned in the other thread. First, you added "degrees" to the slope which is not correct. It is degrees or non-dimensional slope, not "0 degree slope". Second that calculation is the amount of "taper" which must be halved to get the actual slope of the line segments. This tells us nothing we dont already know - that a cylinder (D-d)/L would be zero which means it has zero taper and the line segments which it consists of have zero slope. For a cylinder of non-zero diameter these line segments are still parallel and non-intersecting and the resulting shape has no intersection point/vertex which is required for a cone. The entirety of my response stands as stated with no modifications needed.