I should mention the background of the author:
I'm sure Mr Neumann is a GDnT expert in his own right - I should not have discounted him in that respect. Having said that, it does not exempt him or anyone else from having to back up his statements with supporting logic in the form of direct support from the standard or the geometry/math. The article you posted is notably devoid of this. I really don't care for pitting one expert against another based solely on their qualifications - I don't think this is a worthwhile endeavor, I only presented a counterexample as I thought it should be shown that this is not a unanimously held opinion by well respected experts. I think its much more productive to consider the merits of the arguments themselves.
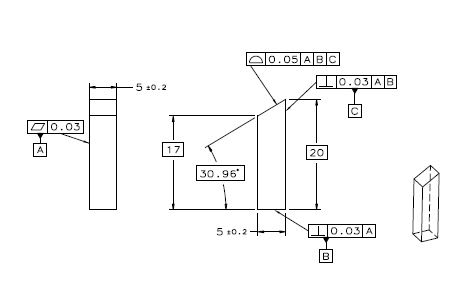
I have not seen a sufficient (nor even remotely mathematcially/geometrically rigorous) explanation by any expert as to why a cone should be considered a FOS. Most of the arguments I've seen boil down to being able to derive an axis - an axis is not a requirement for a FOS as I've shown several times over. An axis only implies symmetry.
A cone is a commonly encountered feature. There are several examples of cones in the Y14.5 standard, none of which are treated as FOS. We're on our second version of the standard which allows for IFOS. As I've said, all signs point to very weak support for cones as a FOS.
In the referenced thread, I don't understand statements like: "Does it have opposing elements? No, they're only partly opposed and never fully opposed so an actual local size is not defined". Doesn't a point on a conical surface face an opposing point on the same surface rotated 180° about the axis?
They don't have opposing elements, "opposing" in this sense meaning in a direction normal to the surface at any point.
A finite conical simulator limited between two specific diameters can expand/contract maintaining a fixed included angle, unlike an infinite fully formed simulator. This is why they are different.
The behavior is the same. Considering part (finite) or all (infinite) of a cone does not change that fact. It only changes the appearance.
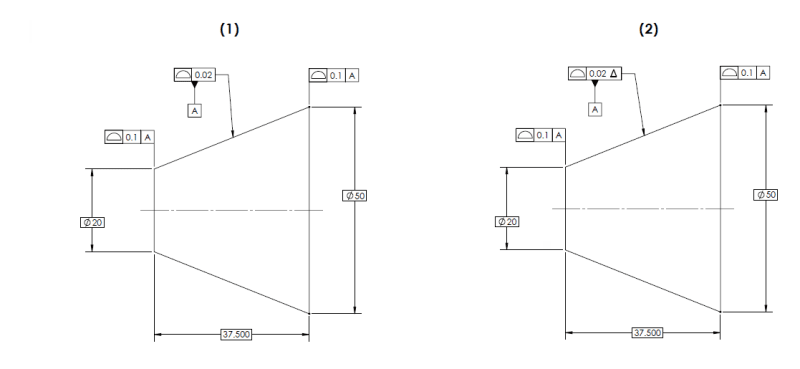
The bolded portion of your Y14.5-2018 citation says: "The function of the dynamic profile is to allow form to be controlled independent of size". This exactly why for many features - in my opinion cones included, form and size characteristics are linked together within a profile tolerance. In many cases this is the default condition, otherwise there would be no need in creating a new modifier to produce independence between the two.
I never said that standard profile doesn't control both form and size for many types of features - such as a cylinder or width-shaped or even IFOSb like the pocket in Y14.5-2009 fig 8-19. I said for a cone considered by itself it doesn't.
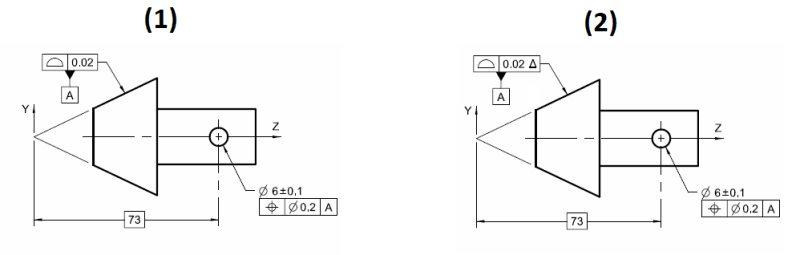
If you believe that profile controls both size and form of a cone considered by itself and that the dynamic profile modifier would separate those two, could you tell me the difference between (1) and (2) below? I see none, but perhaps you do.
The criteria for what features can and can not be FOS should only be looked for in the definitions in the standard. My understanding is that basically all features that can be enclosed or enclose envelopes of form that is either a sphere, a cylinder, a pair of parallel planes or any other closed-form that repeats the theoretical form of the feature can be considered a feature of size.
"enclosed or enclose envelope of form"
"closed-form"
"derive a center point" (from quote below)
Despite your statement that criteria should "only be looked for in the definitions in the standard" only the first one of these three are found (or roughly found - this is of course not the exact wording) in the standard and it is not defined, so we must interpret it. As best I can tell your interpretation for "enclosed or enclose" (or more properly "contain or be contained by") is "touching" - if you have an alternate or more precise definition I would be interested to hear it (I'm not sure how else to interpret your 20 Nov 19 17:29 "As long as it's set, it contains/being contained"). I don't see how this rules out any feature - including a planar one.
The following two are not included in the standard and yet you have mentioned them, and without precise definitions to boot.
Cones are not "closed-form" by any definition I know of. Perhaps you have an alternate one. Regardless, its not included in the standard and without an exact definition I don't see how its relevant.
You have yet to provide a method to derive this "geometrical center".
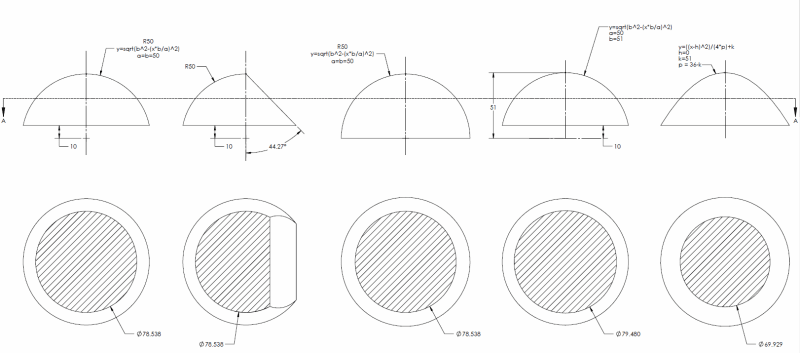
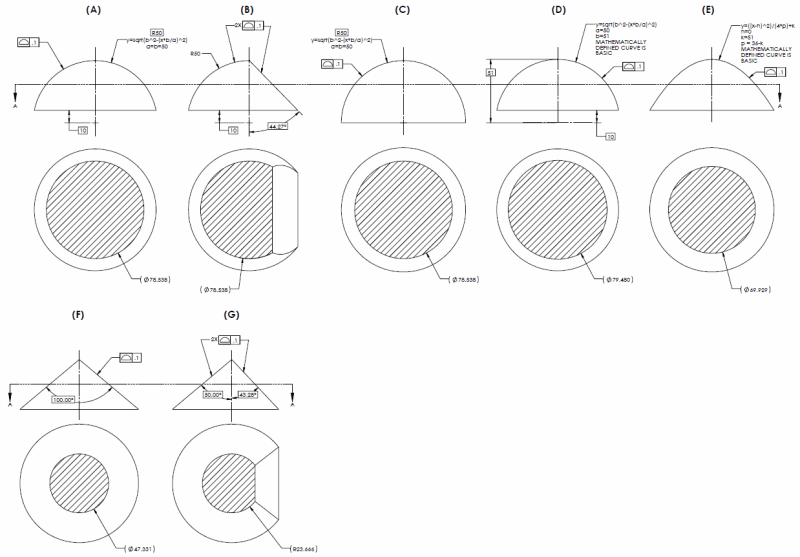
A less-than-half-sphere doesn't have the opposed points needed to derive a center point but arguably one can treat it as a surface of revolution. The issue would be lack of an unambiguous location and orientation of a revolution axis - unlike with the cone there are infinite possibilities. For me, the existence of a defined axis indicates (but not a prerequisite to) the existence of an actual mating envelope.
None of the shapes presented nor a cone have opposing points as I defined above. I've already showed a shape which would not have a defined axis yet you consider an IFOSb - namely a cone with a flat (G). I'm still not clear, do you believe the semi-spherical shapes (A) or (B) to be FOS? If so why?
Your argument, like most considering a cone as a FOS, revolves around the derivation of an axis - which is neither explicit nor implied in the definition for FOS, indeed I have already shown shapes which you consider a FOS without a defined axis. In that case you pivot to derivation of a "geometrical center" - another term not included in the standard's definition of a FOS and I have yet to see your definition for such derivation.
All this means the "WHY" I was searching for is still missing. I am still not clear on WHY you determine one shape is a FOS and another is not.
As a side note on a previous comment:
I don't see how diameters of circular elements on a planar feature can have any meaning.
Y14.5-2009 section 9.4.1 said:
Where applied to surfaces constructed at right angles to the datum axis, circular runout controls circular elements of a plane surface (wobble).