Simulating a datum center plane 2

[semiond]

I need help in understanding this issue regarding simulating a center plane from a datum feature related to an external width dimension: let's say a width dimention is defined as a primary datum feature. When using a vise-like physical datum feature simulator with two almost parallel faces that close on the part, unless the tangent planes on both sides of the datum feature are perfectly parallel (and in the real world they're not), one of the vise faces will act similar to a primary datum plane - touching on 3 high points, and the opposite face will touch on only one point, similary to a tetriary datum plane. Now, depending on which side of the datum feature will make the more stable contact with the simulator, we might get a different separation width between the vise faces, and therefore the simulated datum plane will also be different. For example, if the measurement set up has the vise faces oriented horizontally, the side of the datum feature facing down will orient the part in the fixture, and if you flip the part upside down for a repeated measurement you might get different results on whatever control called out that datum. Now, I understand that there is only one "actual mating envelope" to the datum feature per ASME and only one of the sides facing down will produce the "minimum separation" condition per fig. 4-13, But that means that you have to mount the part twice in the fixtute and re-check your results, and I somehow doubt that this is the recommended practice... on the other hand, if the vise is oriented vertically, we will have no control over which side we stabilize better in the simulator - which is even worse. Everyone's insight will be much appreciated... Thank you!

 

[axym]

Hi All

Here is my best interpretation of the 3 cases that CH sketched:

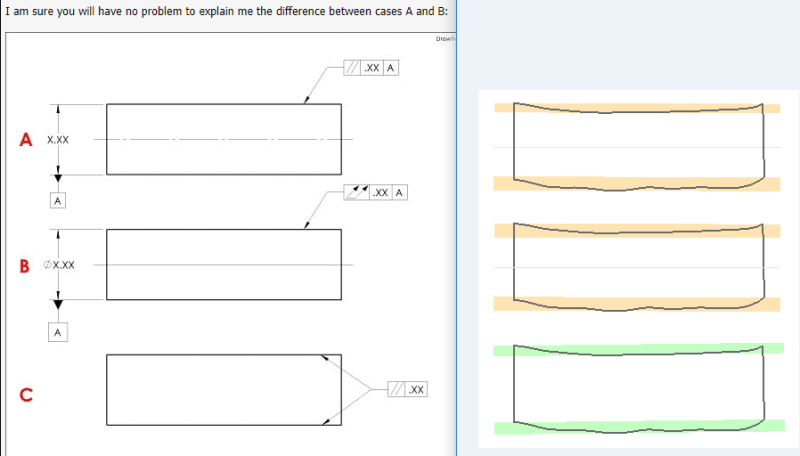
A has two zones, each consisting of two parallel planes. Both zones are parallel to the datum centerplane established from the UAME.

B has one zone, consisting of two coaxial cylinders (shown in cross section). The zone is centered on the datum axis established from the UAME.

C has two zones, each consisting of two parallel planes. The two zones are mutually parallel (or, if you prefer, are parallel to the same arbitrary plane).

It's admittedly hard to tell from these small sketches, but the measured values (thickness of the zones) is different in each case.

Evan Janeshewski

Axymetrix Quality Engineering Inc.

http://www.axymetrix.ca

 

[semiond]

3DDave, this is off-topic, but since you are asking:
Many slotting/slitting cutters can be used in two ways - as a right hand cutter, or as a left hand cutter. You can change the function from RH to LH by uninstalling the cutter, flipping by 180°, mounting it back and changing the direction of spindle rotation.
If you look at one of those cutters from the radial direction, you will see a symmetric geometry resembling the rough contour i showed in the sketch describing the measurement problem.

Most slotting cutters (and cutting tools in general) can be mounted or adapted to the machine in several ways. When used on an arbor of a horizontal mill, they are usually clamped from both sides between spacers - this is why the functional orientation is best established by simulation of a center plane: the datum feature simulator acts like the clamping spacers in the machine.

You asked what are the holes for.
The fact that there are all kinds of different adaptation methods and devices also explains the function of the holes. If you were asking from pure interest, i could go into detail on that. But since interest towards machining equipment is clearly not what motivates you to ask these questions, i will spare my time. Besides, if you posses any basic technical knowledge, you can probably complete the picture yourself.

 

[3DDave]

semiond,

If you have to reverse the spindle after reversing the cutter in order to use the cutter, then that's proof that it isn't symmetrical and the two sides are easily distinguishable. They aren't randomly dropped into a sharpener, right or left, expecting the sharpener to work correctly, so there is a preferred side.

Unless those spacers close in at a single point in the machine coordinate system at the exact same rate then there's no 'center' in the application of the item.

Instead, relative to the spindle drive end, there is a fixed face against which a spacer or stack of spacers is set and then the cutter, and the other side of the cutter acts as a stop for the second spacer(s). No centering at all.

It returns to the point that if you want to confirm the item functions correctly in more than one orientation with a different datum feature as the primary orientation control, then the inspectors need to do the inspection for each orientation.

Nice touch in making a counterclaim and stopping short of backing it up. "Spare my time" indeed.

 

[semiond]

3DDave,
I never heard that choosing a center plane as a primary datum is only valid if there is an accurate centering process in the application - if that's what you think, that's your private agenda.

A center plane is usually chosen to be a primary datum in the following cases:

1. The part is contacted (not necesarrily "centered") on two parallel faces in the functional assembly, and there are features on the part designed symmetricaly to those parallel faces.
2. If the part is contacted in the assembly either on one face or the other without preference (RH/LH cutter for example), and again, there are features that are symmetrical.

I would say the part i'm dealing with is both a combination of those two cases, and each of these cases separately in the same time. By the way it is not necessarily contacted by spacers from both sides. There are other machine configurations as well, and as i said, several mounting possibilities. In some cases the mounting is ckearly one sided.
Yes, checking the part for all controls in two different orientations is probably the one way to cover all cases - i know that. But if you have any experience you should know that these type of requirements are seldom realized into ptactise. We have to find compromises. Maybe it's different in the Aerospace industry, but this is a milling cutter, not a spaceship component.

As for the symmetry issue - i never implied that the part was symmetrical in every possible view projection. I don't know how this is relevant to anything and why you keep mentioning this.

Nice touch in making a counterclaim and stopping short of backing it up. "Spare my time" indeed.

Sorry, is this a debating club here? I didn't know. My bad.

 

[semiond]

C has two zones, each consisting of two parallel planes. The two zones are mutually parallel (or, if you prefer, are parallel to the same arbitrary plane)

Evan, this is a very interesting definition. This means that there can be an optimized reference plane that the two faces have the minimum parallelism deviation from, similary to what you explained about cylindricity.
Is this what the old ISO standard meant?

 

[3DDave]

semiond,

I get reliable results from my efforts. That's my experience. I look at the task and the available process and adapt the design to meet the end requirement. I would not make the description uselessly complicated by introducing parallelism to a derived plane when direct measurement would produce superior results.

Claiming that some closeted industry practice is somehow superior or can't possibly be understood by anyone else is a debate technique. Not a good debate technique, but a debate technique just the same.

"Yes, checking the part for all controls in two different orientations is probably the one way to cover all cases - i know that"

If you know that then what's left?

 

[greenimi]

The standard uses some unfortunate wording in the cylindricity definition. It mentions a common axis, but only for the definition of "cylindricity" which is just the condition of being perfectly cylindrical. The cylindricity tolerance zone is defined as two concentric (the term should be "coaxial") cylinders (with no mention of an axis) within which the surface must lie. It then goes on to mention that cylindricity applies simultaneously to both circular and longitudinal elements, without mentioning elements in the definition or requiring that elements be established at all. Lots of red herrings here - the definition mentions a common axis, circular elements, and longitudinal elements but none of these are actually required! So at the end of the day cylindricity can be applied and inspected without using or defining an axis. It's two coaxial cylinders - we can imagine an axis down the middle, but we don't have to.

Interesting fact about cylindricity's definition.
I remember similar issues are with circularity definition and also with derived median line definition.
The natural question is why only the definitions which have or contain the word axis have problems or they are NOT robust? I do not remember flatness or straightness of an individual line having definition debates

 

[greenimi]

Evan,
Since you are member of the mathematical standard commitee, do you know why a more robust mathematical approach is not discussed and maybe agreed in y14.5 or y14.5.1?
I am thinking that ISO GPS would have a better definitions for those callouts (versus ASME) as this system is well known for the care they have and take for their definitions?
Again, I am thinking specially for circularity, cylindricity and derived median line straightness.

 

[semiond]

If you know that then what's left?

Defining two different primary datums and DRFs and doubling all controls is not a realistic solution in my case. It's not a new product and the drawings are not defined according to any valid standard, but we get no complaints on functionality. I'm trying to introduce a change that involves proper definitions, and won't make inspection more time consuming. If the change will be understood as something that slows or complicates things, it won't happen. One solution could be defining one of the clamping faces as a planar datum and controlling the other for parallelism, orienting the part at inspection according to one functional interface, and trusting on the parallelism to take care of the other scenario. But, the planar datum solution doesn't really supply an answer on the question how to position the body width symmetrically to the clamping faces. To control the symmetrical position properly, UAME centerplane is still needed.

 

[3DDave]

semiond,

Then it won't happen, will it? You already know that finding the centerplane is defective.

Your latest solution is one I already gave you. If the process can't produce a suitable parallelism, which could easily be below 0.02mm and should be 0.002 mm, then you need competent machinery, not a new theory to cover for defective parts.

 

[semiond]

0.002 mm parallelism tol. for surface grinding, on the relevant surface areas - absolutely crazy. But thanks for the tip.

 

[3DDave]

Here's a typical, from a guy with an order for a dozen or more parts to match thickness. Bagel sized parts, 5mm thick, acceptable variation was +/-.0005 inch, but customer wanted a better match between the members of the group.

"The parts came in this afternoon.
All looked great.
With a micrometer, they did not vary more than .0001"
As best as I can measure, ... and that will be good enough for the customer.

The second time around for these parts, took a little moral support for the outsourced shop.
Talking to the supervisor, not the machinist.

They used (some of) the suggestions here, (well the reasonable ones, anyway,) and we got some nice looking parts.

Thanks everyone.

Time to start another thread about one of the (many) other adventures for today."

If readily achievable tolerances is crazy, then how bad off is your production line?

 

[semiond]

3DDave,
That's a nice story and sounds like they've done a good job. Can't make any conclusions out of it because:
1. Micrometer measurement - actual local size. Not parallelism.
2. What was the machining process? Lapping? Grinding? Milling? Different processes mean different manufacturing costs, different pricing for the customer, and different achievable tolerances.
3.What was the ID and OD of those bagels? (Total variation of a machined surgace is related to surface area).
4. What is the workpiece material and what are it's properties? Is it an abrasive tool steel, or perhaps - free machining steel? For a given time available for a project, you can achieve better accuracy if you're machining something that allows you to make more passes and take smaller depths of cut each time.
5. How were these items priced? Money buys time, time allows slower feeds and more passes = tighter tolerances.

 

[3DDave]

Semiond,

You can use Google to find the entire exchange.

But if this is a result your company depends on, it would be a really good idea to be good at it.

I found dozens of examples for supporting this as readily in range for surface grinders.

But, back at you - questions you have not answered for your own parts:

2. What was the machining process? Lapping? Grinding? Milling? Different processes mean different manufacturing costs, different pricing for the customer, and different achievable tolerances.
3.What was the ID and OD of those bagels? (Total variation of a machined surgace is related to surface area).
4. What is the workpiece material and what are it's properties? Is it an abrasive tool steel, or perhaps - free machining steel? For a given time available for a project, you can achieve better accuracy if you're machining something that allows you to make more passes and take smaller depths of cut each time.
5. How were these items priced? Money buys time, time allows slower feeds and more passes = tighter tolerances.

 

[semiond]

I thought that since you brought a reference case you might as well have the basic relevant background information. I don't see how returning these questions back to me now can serve any purpose. If you intend to offer consulting on improving grinding processes based on my answers, i think i'll skip that, thank you very much.

 

[axym]

Evan, this is a very interesting definition. This means that there can be an optimized reference plane that the two faces have the minimum parallelism deviation from, similary to what you explained about cylindricity.
Is this what the old ISO standard meant?

semiond,

I'm not sure if this is what the old ISO standard meant or not. I would say that there would be applications where the datum-less parallelism would capture the functional requirement - the width feature as a primary datum feature may be one of them.

Interesting fact about cylindricity's definition.
I remember similar issues are with circularity definition and also with derived median line definition.
The natural question is why only the definitions which have or contain the word axis have problems or they are NOT robust? I do not remember flatness or straightness of an individual line having definition debates

greenimi,

I don't think that the references to the word "axis" are the problem. I would say that the cylindricity definition is robust - the tolerance zone is well defined. It's just that the definition mentions some things (elements and a common axis) that are not necessary. The flatness definition is robust (as far as I know), but the defintitions for circularity and line element straightness have some issues. Don't get me started on derived median line straightness ;^).

do you know why a more robust mathematical approach is not discussed and maybe agreed in y14.5 or y14.5.1?

This might be the most complicated question of all ;^). Form tolerances are not as simple as they appear to be. I would say that the element-based form tolerances (straightness and circularity) are the most complicated tolerance types in Y14.5 (other than actual local size), once you get down to applying the tolerance to actual part geometry. The Y14.5 definitions (and especially the figures) are simplified to a certain degree - they do not fully acknowledge the complexity that arises. Certain details in the definitions need to be clarified before a more mathematical approach can be meaningfully applied.

Evan Janeshewski

Axymetrix Quality Engineering Inc.

http://www.axymetrix.ca

 

[semiond]

. I would say that there would be applications where the datum-less parallelism would capture the functional requirement - the width feature as a primary datum feature may be one of them.

I agree. This could be a way to qualify a primary datum feature of width.
To qualify a primary planar surface datum feature, flatness is usually applied.
To qualify a primary cylindrical datum feature (RMB), i suppose cylindricity can be the answer.
For a primary width datum feature (RMB), it is probably "mutual parallelism" if such thing will be allowed.
Seems like it won't be an easy conrol to inspect without CMM though.

 

[pmarc]

I would say that there would be applications where the datum-less parallelism would capture the functional requirement - the width feature as a primary datum feature may be one of them.

Another one could be datum-less parallelism used as a refinement of datum-less position tolerance applied to primary pattern of holes/cylinders or slots/tabs.

 

[3DDave]

I don't see the form tolerances as complicated at all. They are fundamental and trivial.

What is complicated is trying to convert inaccurate measurements of inaccurate parts into a unique value regardless of how those measurements are made, which then drags in the notion of what it means to have a minimum deviation calculation. In contrast, conformance is straightforward pass/fail.

What seems even more complicated is to justify, by eliminating information by axial and planar simplifications, that all the effects of that information can be ignored. It's a form of averaging - take a set of values, apply some averaging function, and therefore lose what the original values are. It's suitable if one is looking for statistical outcomes, but on a single part or single group of numbers, the original basis often cannot be ignored.

Just because a mid-plane can be derived from a heavily tapered part, it doesn't mean that the part will be sufficiently constrained between parallels. There's no mechanical process that duplicates that, so it has no physical meaning. Allowing the basis to have more variability than is allowed to the features that depend on it is recognized as a poor practice.

The typical coping mechanism for variability is to make the form errors small enough that the part is within the elastic deformation limits for all the parts involved and to make those deformations cause translation changes, not orientation or twist changes.

 

[semiond]

Another one could be datum-less parallelism used as a refinement of datum-less position tolerance applied to primary pattern of holes/cylinders or slots/tabs.

Similar to the composite tolerance concept, only with both segments' tolerance zones independed of any external datums - interesting.