Slot in plate - best end shape for minimum stress?

[dculp1]

The image shows a plate with a 10mm wide slot. In this design the slot's end shape is a 20mm x 10mm ellipse. A uniform tensile load is applied to the plate's top surface (the narrow surface at the top of the image). Compared to a slot with an R5mm end shape, the von Mises stress is 23% lower.

Besides an ellipse (and possibly a polynomial), what other end shapes should I consider in order to minimize the stress? (I seem to recall a shape that approximated the surface streamline of a fluid flowing through an orifice but I haven't been able to find this again.)

Thanks,
Don C.

 

[Jboggs]

Meanwhile the machinist that has to make this thing is shaking his head at these egghead engineers who will spend days trying to achieve the "perfect" (but unfeasible) design without ever thinking about the fact that in the real world the "near perfect" (but much more feasible) design will work just fine at a tiny fraction of the total cost to design and build it. Apply a real world safety factor, cut a standard milled slot, and move on to other problems. Just sayin...

 

[rb1957]

"machinist" ? ... haven't known CAM machines to complain ...

another day in paradise, or is paradise one day closer ?

 

[dculp1]

The boundary conditions are shown as the pyramids in the image (frictionless supports). The meshed FEA is a 1/4 model of the entire plate which accounts for the frictionless supports on the back side.

The load on the face is -1MPa. This is just a nominal tensile load in order to compare the stresses from various slot configurations. In the actual use (vibrating resonator-horn) there are no applied loads. All of the stresses result from the vibrational inertial loading (F=m*a).

Please keep in mind that this static model is just a simplification of a dynamic situation. Please refer back to my original post -- in the static model that I created, is there a better slot configuration that will reduce the stress better than the ellipse (regardless of whether you feel that this static model is appropriate for the actual situation)?

 

[dculp1]

I wouldn't rule out shot peening. However, this involves empirical testing (shot material, shot size, velocity, impingement angle, etc.) Also, I'm not sure how the deep slots could be shot peened (e.g., a slot that goes through 300 mm. Thus, my first approach is to get the lowest possible stress through geometry modifications.

 

[dculp1]

Jboggs --

I welcome your ideas on how to apply a "real world factor of safety". The only way I know to do this (for this application) is to reduce the vibrational amplitude and the associated vibrational stresses. However, then the resonator-horn would no longer perform it's intended function (plastic welding, among other uses).

 

[rb1957]

"real world factor of safety" ... this is the safe life factor you apply, to ensure you don't get failure in service. Maybe you replace "for cause" ... after a fatigue crack has developed ?

I'd research ultra high cycle fatigue to understand the mechanism better. Inclusion mobility, the typical fatigue mechanism causing cracks to develop, is maybe operating in an unusual way. It looks like you're applying much lower stresses than I'd consider (with a cycle rate of 1 Hz)

another day in paradise, or is paradise one day closer ?

 

[dculp1]

rb1957 --

Once a crack in these resonator-horns is initiated it propagates to to failure almost immediately (typically within a few seconds). Then the frequency drops unacceptably low and the system shuts down. There is no ability to monitor crack growth and make preventive replacement.

Having worked with power ultrasonics for 50 years, I'm familiar with high cycle fatigue (in the range of 20 kHz - 100 kHz). I have tested samples at ultrasonic frequencies to develop S-N curves for titanium and various aluminums. At 20 kHz, 5e8 cycles occurs in about 7 hours of continuous sonics so stress cycles accumulate very rapidly. Given this, the titanium horns should be designed for essentially infinite life (stress below the S-N knee) and aluminum horns should be designed for long life (no S-N knee).

As I mentioned earlier, "The load on the face is -1MPa. This is just a nominal tensile load in order to compare the stresses from various slot configurations. In the actual use (vibrating resonator-horn) there are no applied loads. All of the stresses result from the vibrational inertial loading (F=m*a)." For comparison purposes I could have chosen any load on the face. I chose -1MPa for convenience.

 

[3DDave]

The OP is too modest for our own good:

http://krell-engineering.com/fea/fea_info/fea_resonator_design.htm

Shot peening is little different than shooting a gun with tiny bullets in huge numbers. Any surface that is visible in a straight line from the outside of the part is a candidate. Changes in impact angle can be offset by changes in shot velocity or duration - a specialist in shot peening will have better suggestions for exact details.

I wonder how much of the stress that is seen is from the way the loads are applied - I see how tension is put on the one surface, but how is it resisted by the remainder of the material? It doesn't seem likely that the thin section at the top of the slot would have the same load as the rest of the face.



How To Ask Questions The Smart Way

http://www.catb.org/~esr/faqs/smart-questions.html#intro

 

[LiftDivergence]

Hi dculpt1,

I've been thinking about his a bit and this may be redundant given some of the other advice you've received. But here are some things I would consider:

1. We know you are designing this for a fatigue application. That does not invalidate your static stress application though. For fatigue, we are not explicitly interested in the Kt (static stress concentration factor. Moreso we care about Kf, the fatigue stress concentration factor. That being said, the two are related via the notch sensitivity. So immediately you may be able to improve the performance by selecting a material with better Neuber constant, "a". Although you might be locked in. Furthermore, the notch sensitivity is also influenced by the radius.

You can also change the Neuber constant by changing conditions (annealed or strain hardened vs heat treated, etc).

2. Improvements to the local stress can also be made by introducing residual stresses. Shot peening has been discussed above. But there are many other ways to achieve this including:

-through hardening​

- case hardening​

-cold forming​

-laser peening​

-other methods of mechanical prestressing compressively in the axis you know the part is loaded in​

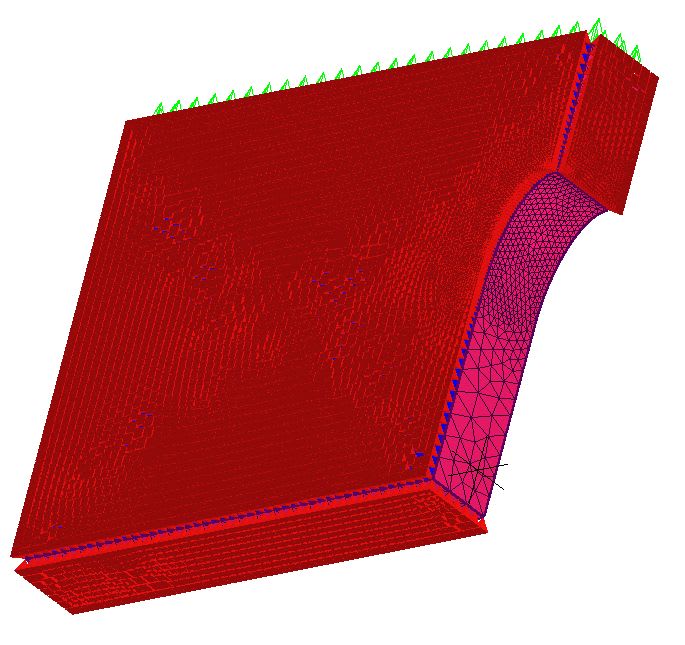
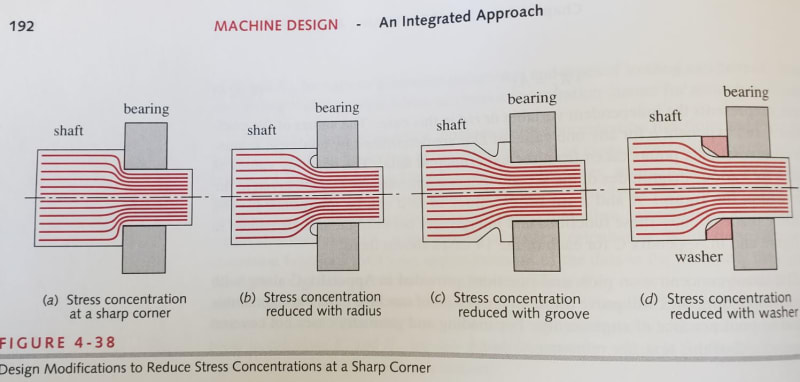
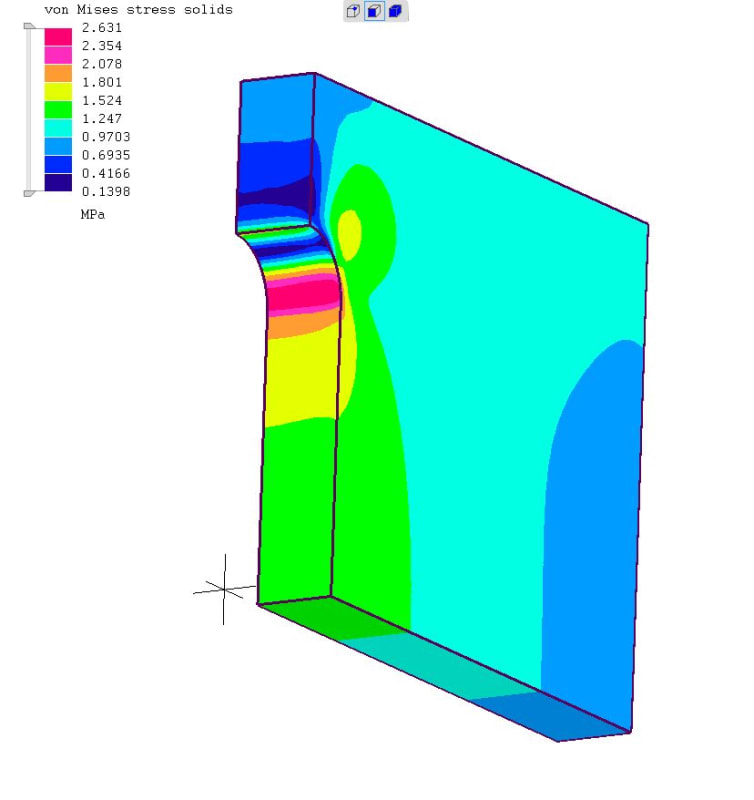
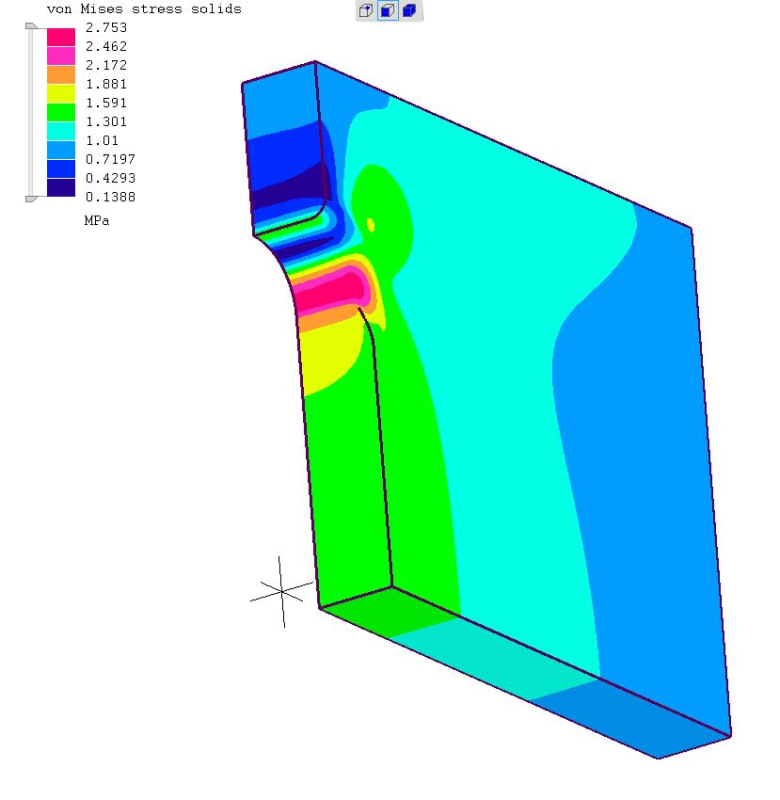
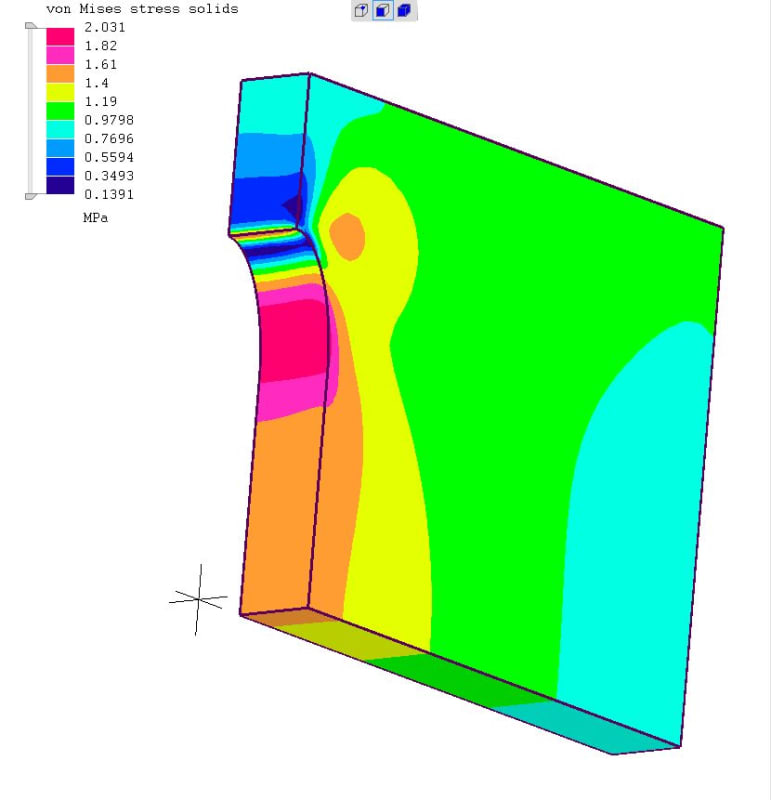
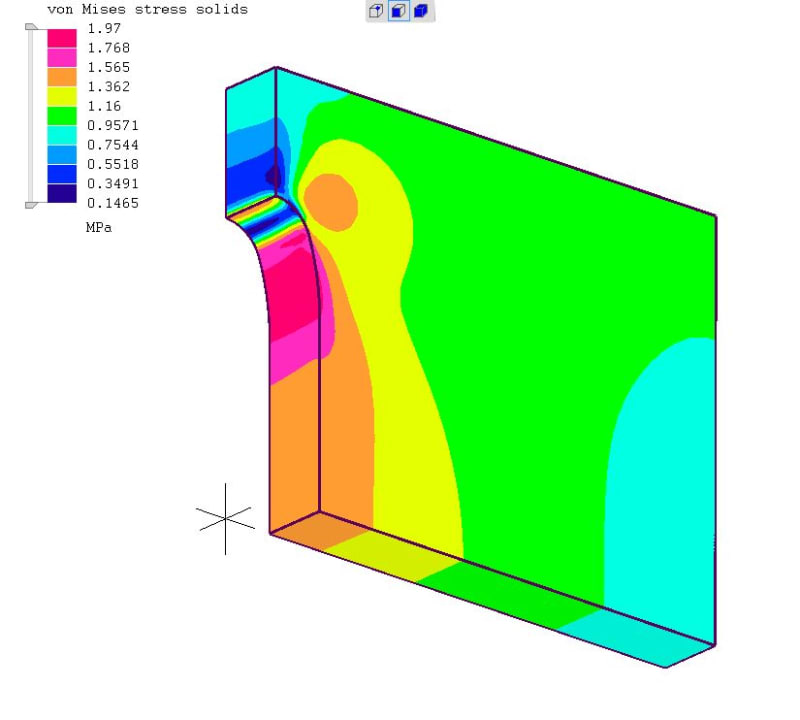
3. There are more ways to change the local stress field other than altering the tip radius. The "flow" analogy you mentioned is alluded to in this figure from Norton. It is not really what you have, but gives the idea.

The crux of the stress riser problem is twofold:
1. The reduction in net section area causes a higher stress because, well, the cross section is smaller
2. The eccentricity of the load path ie "flow" diversion causes some effective bending...think about the load path and the crystal lattice.

You could possibly mitigate Item 1 by providing more material to take the load. The notch tip causes a concentration, but this could be somewhat offset if the cross section was greater in that area. Is there any reason you cannot slowly ramp up the width or thickness to be greatest in the cross section of the notch tip?

Finally, you said you have Peterson... if it is the Pilkey version, have a look at Section 4.5.1, page 225:

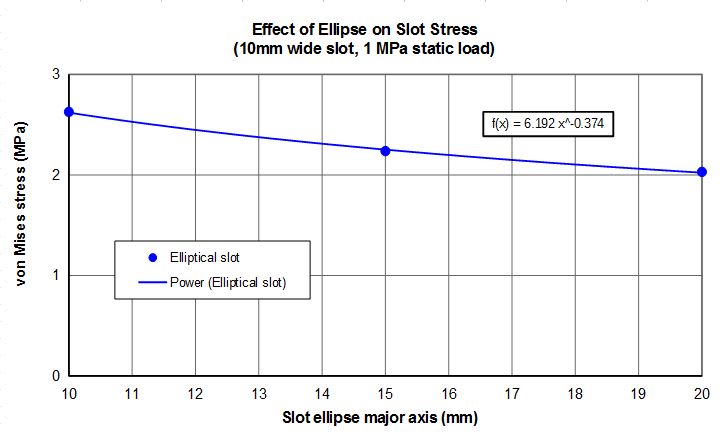
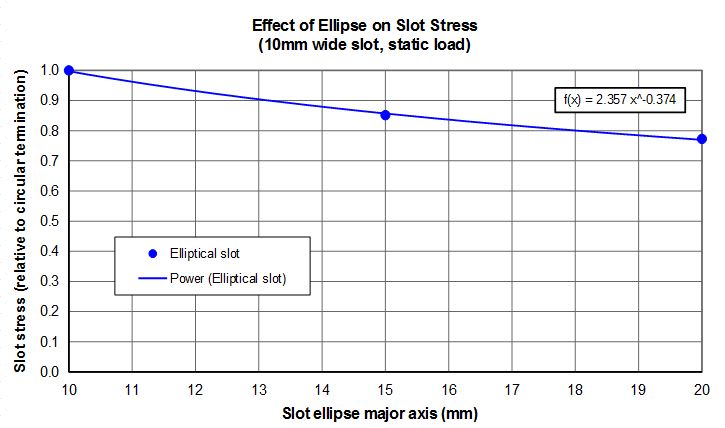
A photoelastic investigation (Durelli et al. 1968) of a slot of constant a/b = 3.24 found
the optimum elliptical slot end as a function of a/H9 where H is the panel width. The
optimum shape was an ellipse of a/b about 3 (Chart 4.59), and this resulted in a reduction
OfKtn, from the value for the semicircular end of about 22% at a/H = 0.3 to about 30% for
a/H = 0.1 with an average reduction of about 26%. The authors state that the results may
prove useful in the design of solid propellant grains. Although the numerical conclusions
apply only to a/b = 3.24, it is clear that the same method of optimization may be useful
in other design configurations with the possibility of significant stress reductions.

However, you'll notice chart 4.59 does not have the stress orientation you desire. That being said, there is a biaxial stress effect in Chart 4.55 which shows that the Kt will reduce when biaxial stresses are present. So you could also control the peak stress by introducing some other load.

Keep em' Flying
//Fight Corrosion!

 

[dculp1]

LiftDivergence --

1. The available materials are limited, particularly by acoustic properties. Steel has good fatigue strength but high acoustic loss. Ti-6Al-4V has relatively low acoustic loss and fairly good fatigue strength (also medically compatible) but is expensive and somewhat difficult to machine. Aluminum (7075-T6) has low acoustic loss and is easy to machine but has relatively low fatigue strength. Through many years these materials have been established as near optimum. (See

http://ultrasonic-resonators.org/materials/materials.html)

2. Some of these can be considered, depending on the resonator material).

The blade ends of bar horns (where slot failures occur) are typically slab milled (

http://krell-engineering.com/fea/industr/industrial_resonators.htm).

Increasing the thickness at the slot ends would significantly increase the machining cost. For thick blades (40 mm at 20 kHz), a reduction in surface stress near the slot-end modification might have little effect since the crack would just initiate farther to the interior of the slot where the modification has little effect.

For block horns (those with intersecting cross-slots), failures always occur at these slot intersections so a modification of the slot at the horn's exterior surface wouldn't be helpful. (BTW, this is one reason that I'm looking at a geometry change at the slot end. If this is helpful for bar horns then I suspect that it would be doubly helpful for block horns.)

I looked at the Pilkey info that you suggested but I don't think that it's useful for my situation.

The figure shows the current FEA results for a slot with elliptical ends.

At this point what I need to find are other curves where the curve is tangent to two perpendicular lines (the slot side wall and the slot end). A circle and ellipse fulfill this requirement but there must be others.

Machining -- I think broaching of the slot ends should be possible for aluminum horns. I don't know about broaching of titanium, especially for very deep slots. EDM is possible but must be very gentle to avoid pitting and residual stresses that would reduce the fatigue life. With this constraint, EDM has been found to be considerably slower than conventional machining. End milling would work but only for limited depths.

 

[dculp1]

3DDave --

See the following animations which are for the actual application (not the preliminary static analysis of this post). The horns vibrate in the completely free condition (no constraints). Momentum is conserved across the dark nodal planes (m*v in the positive direction is balanced by M*V in the negative direction).
Note how the slots deform.

http://krell-engineering.com/fea/industr/barhorn/h102a3_animate.htm

http://krell-engineering.com/fea/industr/blockhorn/h103a3_animate.htm

 

[Tmoose]

I've been bitten by 1/2 and 1/4 models more than once for stress work. Some models were mine, and some were others', but in each case I was the one that received the flesh wounds.
If it were my model I'd be concerned the attachment of a uniform tensile load to that entire face //may// not be very realistic.
With max stress of ~ 2X nominal it seems like a near optimum design.

I'd look at the ( Y ? )displacement of the uniformly loaded surface, expecting it may hump up above the slot, and wonder if that is realistic.

Not knowing the actual arrangement, I'm left to speculate -
- The representation of the plate is accurate as shown, and the uniform tensile load is applied at the interface/faying surface by another component, somehow without enforcing a uniform displacement.
- The representation of the plate is accurate as shown, and the tensile load is applied at the interface/faying surface by another component incapable of enforcing a uniform displacement. Hydraulics could apply such a uniform compressive load to a surface. Tensile ......?
- Less likely guess - the plate extends upward quite a bit farther and the model was cut short for simplification. Then I'd extend the model full length and run it again.

Sometimes it is fun to also look at principal stresses and their directions, even for ductile materials.

---------------.
Here is a pretty crude model of a full plate One edge restrained/fixed. A uniform load ( I think) along the opposite edge. The slot appears to be a much smaller proportion of the model the the OP.
There is no scaling, but the other examples on that page are VonM stress.

https://mentoredengineer.com/wp-content/uploads/2020/02/Full-Radii.png

 

[SWComposites]

Get a 30 trial license for an FE code with shape optimization capability.

 

[dculp1]

Tmoose --

See my reply to 3DDave (just above your reply) for the actual application. As noted elsewhere, my static model is a quick ballpark try to see if modifications to the slot geometry can reduce the slot stress in the actual vibration situation. After I have pinned down potential geometries (possibly in addition to the ellipse) I will model some actual horn-resonators.

 

[dculp1]

SWComposites --

Do you have particular FEA recommendations, considering the objectives of my project and the steep learning curve for most FEA?

 

[dculp1]

Tmoose --

For fatigue (aluminum, titanium, steel) I always look at von Mises stresses. What additional information would principal stresses provide?

 

[dhengr]

Dculp1:
I’ll bet you would accomplish more with a circular slot termination, which would be relatively easy to machine. Then, or at the same time, with the tool shape, machine a radius on the top and bot. edges/corners of the slot all around, and finally polish the entire machined surface. Maybe that’s rolling, burnishing and cold working. For the fun of it, you might try an ellipse with its long axis in the 10mm width direction of the slot. But, this is such a fickle problem that a few mis-oriented material crystals on the slot surface can be the trigger.

 

[dik]

Does polishing the slot minimise stresses, too?

Rather than think climate change and the corona virus as science, think of it as the wrath of God. Feel any better?

-Dik

 

[dculp1]

For a slot with a 5mm end radius (#1 below), I looked at putting a R1.5mm fillet around the radius (#2 below). Interestingly, this increased the stress by about 5% at the surface for this 13mm thick model. However, since cracks often initiate at corners (especially due to machining imperfections), a fillet may actually be beneficial. This must be evaluated by empirical testing.

Polishing the surfaces doesn't minimize the stresses. However, the improved surface finish can significantly improve the fatigue life.

I suspect that a transverse ellipse might actually increase the stress. In any case it would probably not be helpful for other performance parameters in the actual vibrating application.

The following images show the design optimization. In #3 and #4, note how the red stress area has broadened compared to #1 and more of the adjacent material is now stressed to carry the load (e.g., the yellow color). At this point #4 would be preferred since the end (fixed R4.0mm) can be drilled rather than milled (gun drilling - faster and straighter for very deep slots). I think #4 may be close to a practical optimum.

1) Model with R5mm slot end (standard configuration)

2) Per #1 but added R1.5mm fillet - 5% stress increase compared to #1

3) Model with elliptical end (20mm major axis) - 23% stress reduction compared to #1

4) Model with compound tangent radii end (R4.0mm at end, R22.5mm transition to sidewall) - 25% stress reduction compared to #1

 

[rb1957]

I personally think we're barking up the wrong tree.

Who has experience with ultra high cycle fatigue ? We're proposing solutions that work with low and medium cycle fatigue. We understand reducing stress, cold working, shot peening, etc but how applicable are they to this fatigue loading ? If 300psi (I think I remember that number somewhere in this thread) is enough to drive a crack creation, then these something else going on (since this stress is well below any sort of threshold). I think we need to understand the mechanism before we can reasonably suggest solutions.

But your current experience should be enough to determine the useful fatigue life.

It may be possible to develop some servicing program ... cycle for X hours, inspect with HFEC and if you detect a small defect, scrap. Though I suspect you'd be very lucky to detect a measurable defect.

Another option maybe to cycle for X hours, then in a lab, apply a limit load to prove no defect present, then good for another X hours ?

another day in paradise, or is paradise one day closer ?