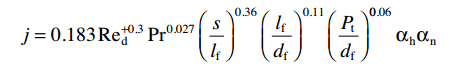Dear all,
I think the ESDU Correlation to get the j number in the book HEAT EXCHANGER DESIGN HANDBOOK written by T.KUPPAN (in both editions) is wrong, or maybe it is a printed mistake.
I think it should be Re^(-0.3) instead of Re^(+0.3) in this equation.
Since I cannot find more support information about this, could you please give me more information about this correlation.
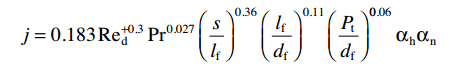
I think the ESDU Correlation to get the j number in the book HEAT EXCHANGER DESIGN HANDBOOK written by T.KUPPAN (in both editions) is wrong, or maybe it is a printed mistake.
I think it should be Re^(-0.3) instead of Re^(+0.3) in this equation.
Since I cannot find more support information about this, could you please give me more information about this correlation.