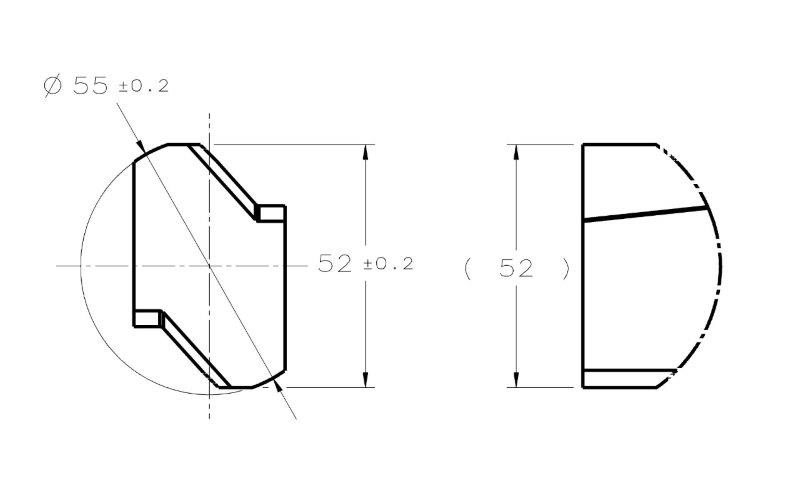
I may be missing something but I can only imagine that a stable minimum envelope for a width feature will always consist of a tangent plane contacting at least 3 high points and a plane parallel to the tangent plane contacting at least one high point.
I am going to ignore the word "tangent" for a moment and concentrate on the "stable minimum envelope" and contact point subject.
For the 2-dimensional case, I will define the following:
Condition 1: One surface contacts the envelope at two points (call these a1 and a2) and the other surface contacts the envelope at one point (call this b1).
Points a1p, a2p, and b1p are the orthogonal projections of points a1, a2, and b1 onto the envelope midline.
Condition 2: Point b1p is between points a1p and a2p.
For the 3-dimensional case, I will define the following:
Condition 1 (option A): One surface contacts the envelope at three points (call these a1, a2, and a3) and the other surface contacts the envelope at one point (call this b1).
Condition 1 (option B): One surface contacts the envelope at two points (call these c1 and c2) and the other surface also contacts the envelope at two points (call these d1 and d2).
Points a1p, a2p, a3p, and b1p (option A) or c1p, c2p, d1p, and d2p (option B) are the orthogonal projections of points a1, a2, a3, and b1 (option A) or c1, c2, d1, and d2 (option B) onto the envelope midline
Condition 2 (option A): Point b1p is within the triangle having points a1p, a2p, and a3p as vertices.
Condition 2 (option B): The line segment connecting points c1 and c2 crosses the line segment connecting points d1 and d2.
I'd say a stable minimum envelope is one that corresponds to a local minimum on the width vs. angle plots I've been posting. Such an envelope will always satisfy conditions 1 and 2. I think it's more useful to look at these conditions as consequences instead of requirements though.
Is something like the below what you had in mind?
In you example, both boundaries of the minimum-width envelope are valid tangent lines. See ASME Y14.5.1M-1994 para. 4.3.2 regarding candidate datum sets for nominally flat datum features, although that definition must be converted to 2D for the examples we're looking at here.
I had in mind a feature such as the following:
[pre]
surface 1:
point 1: (0.00, 0.40)
point 2: (1.00, 0.40)
point 3: (2.00, 0.37)
point 4: (3.00, 0.35)
point 5: (4.00, 0.34)
surface 2:
point 6: (0.00, -0.40)
point 7: (1.00, -0.40)
point 8: (2.00, -0.37)
point 9: (3.00, -0.35)
point 10: (4.00, -0.34)[/pre]
The minimum envelope width is 0.80, obtained with contact at points 1, 2, 6, and 7. For each surface, all contact points are within (1/3)*(4.00-0.00) of one end. This means that neither boundary is a valid tangent plane per the ASME Y14.5.1M-1994 definition.
An envelope width of 0.819836 can be obtained with contact at points 2, 5, and 6 (or 1, 7, and 10), and the boundary that contacts two points is a valid tangent plane. This is the smallest envelope that meets the additional requirement, but it not stable in the sense described above.
pylfrm