Basic determinacy question on a braced frame

[StrEng007]

Got into a debate on this and would like some input.

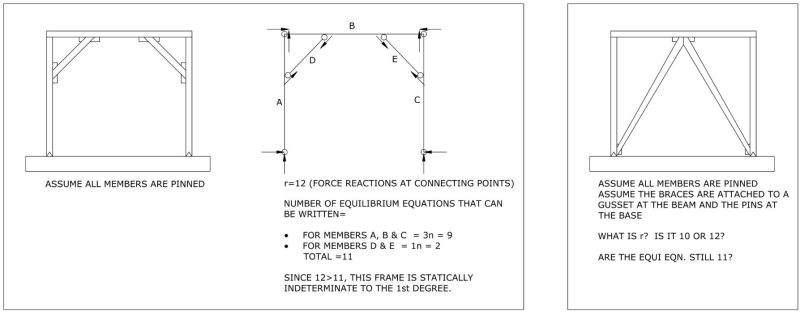
Using the general approach for determinacy on a FBD (r vs. 3n), I've presented two separate cases of a braced frame below. The first situation utilizes kickers that are located at frame corners. The kicker is assumed to develop an axial load only and only provides (1) equation of equilibrium as illustrated below. From what I see, this frame is statically indeterminate to the 1st degree. Is there any other way to quickly solve this 1st degree of indeterminacy without having to assume inflection points as we do using a portal frame method approach? Also, I don't want to consider a roller at one of the bases.

Using the same approach for counting the number of force reactions and equations of equilibrium, is the second frame unstable, determinate & stable or determinate & unstable.

NOTE: The horizontal beam is continuous in both examples. Each individual column is continuous in both examples.

Thanks!

 

[rb1957]

I don't think sketch 2 is redundant, since you can relate the kicker load to the ground reaction.

because the verticals are pinned at the horizontal, now the verticals are simple beams (zero moment at each end, a point load on the span). therefore the ground reaction is a proportion of the kicker (solve the vertical like a simple beam, yes?)

another day in paradise, or is paradise one day closer ?

 

[klaus.]

Number 2 is one time indetermined
Take one kicker away and the system is still stable



best regards
Klaus

 

[rb1957]

if you take one kicker away you'll have a mechanism (as you've got pinned joints). If you have fixed joints between the horizontal and the verticals then you wouldn't need either kicker and you'd have a stable frame.

another day in paradise, or is paradise one day closer ?

 

[jdgengineer]

Sketch 2 is still stable if you remove one kicker. Sketch 2 is a moment frame not a braced frame. You could replace the kicker with a fixed joint for the purposes of visualizing determinacy.

 

[Once20036]

"Is there any other way to quickly solve this 1st degree of indeterminacy...?"
What loads are you resisting? Horizontal? Gravity?
Assuming that loading is symmetric, I would assume that the horizontal forces for each load case are the same at each pin. This leaves you with 3 unknown reactions and 3 equations for equilibrium.

"...is the second frame unstable, determinate & stable or determinate & unstable?"
Indeterminate and stable. I would solve with the same assumption as Sketch 1.
I believe that sketch 2 is stable if you remove one diagonal, as Klaus stated above. This has nothing to do with moments frames as sketch 2 indicates that everything is pinned

 

[jdgengineer]

Once20036, a knee-braced frame behaves as a moment frame. Yes, all the joints are pinned, but the knee brace creates moment couples to essentially provide fixity at the joint and resolves forces in a similar way as a moment frame, and not really like a braced frame. Draw the moment diagrams if you don't believe me.

If this was a steel frame, you would have to meet requirements of ordinary moment frame. See commentary to E1.2 of AISC 341-10.

 

[XR250]

#2 is determinate for all practical purposes as the brace axial stiffness will significantly Trump the beam bending stiffness.

 

[jdgengineer]

#2 is indeterminate as is any standard moment frame with fixed ends on each side of the beam. If you assume the columns have the same stiffness you can solve using portal method by assuming half the reaction is resolved by each pin support. You would then explode the frame and solve the FBD for each individual member.

 

[XR250]

#2 is indeterminate as is any standard moment frame with fixed ends on each side of the beam.

The detail says that the members are pinned.

 

[jdgengineer]

Knee braced frame = moment frame.

 

[rb1957]

a portal frame, with fixed corners, is redundant.

but in this frame, because the corners are pinned, we can relate the kicker load the ground reaction (because the vertical is a simple beam). but ...

now I can see the frame is still a structure if you remove one kicker (which says that's it's singly indeterinate). It's not a mechanism because the parts rotate about different centers. Which would imply that a portal frame with one fixed corner is determinate.

another day in paradise, or is paradise one day closer ?

 

[BAretired]

Using the general approach for determinacy on a FBD (r vs. 3n), I've presented two separate cases of a braced frame below. The first situation utilizes kickers that are located at frame corners. The kicker is assumed to develop an axial load only and only provides (1) equation of equilibrium as illustrated below. From what I see, this frame is statically indeterminate to the 1st degree. Is there any other way to quickly solve this 1st degree of indeterminacy without having to assume inflection points as we do using a portal frame method approach? Also, I don't want to consider a roller at one of the bases.

I agree that the frame is indeterminate to the first degree. The simplest way to solve the problem is to consider one base support to be a roller. I don't know why you do not wish to consider that.

Another way to solve the problem is to remove one of the "kickers" and solve the resulting three hinged arch for the applied forces, calculating the change in angle at the beam/column junction where the kicker was removed. Then apply a unit load parallel to the kicker to the beam and also to the column and determine the change in angle at the beam/column junction from this effect. Then calculate the force required to restore the angle to 90^o. Messy...I prefer the roller solution.

BA

 

[jdgengineer]

BAretired, why would you want to make the frame determinant? Don't you want a reaction at the base of each column? If you put a roller, it's the same thing as only welding one side of the beam in a moment frame. You may make it determinant, but you've lose some redundancy. I think the indeterminancy isn't a problem. Assume each reach takes 1/2 the load and then solve with FBD from there as it is determinant.

 

[StrEng007]

The reason I don't want to assume a roller, in order to make this a determinate system, is that I want to be able to apply any loading scenario to this braced frame in either direction. It seems like we all agree that the first sketch is stable and inderterminate to the 1st degree.

Regarding the second sketch, Since the kicker is attached "at the pin", I see the number of force reactions at this location as 2. However, that would sum the total number of force reactions as 10 (2 at pinned base, 2 at pinned base, 2 at corner, 2 at corner, 1 at kicker to beam gusset, 1 at kicker beam gusset. This is compared to 11 equations of equilibrium, and is unstable by one degree. However, looking at sketch 2 it logically seems stable. This braces frame is almost categorized as truss since each member is pin connected at its ends EXCEPT that the gusset is located at the beam mid span which requires us to use the r vs 3n rule (instead of b + r vs 2j).

When you design a chevron frame, do you assume fixed corners? How do you solve a chevron by hand?

 

[BAretired]

jdgengineer,

Making the frame determinate is a technique to solve for the forces in the frame. I am not suggesting that the actual frame be changed. The idea is to imagine a roller replacing one of the base hinges thus making the frame determinate, then calculate the horizontal movement of the base for the determinate structure, then calculate the force required to push it back to where it was. In that way, the unknown horizontal force can be solved for the indeterminate structure. It is one of several methods of solving a frame having a single degree of indeterminacy. Some engineers call it the "Dummy Unit Load Method".

Of course, if you have a 2D frame program, none of that is necessary.

BA

 

[jdgengineer]

Got it BAretired, I understand what you were proposing.

Guys, I'm sounding like a broken record here, but Sketch #2 is NOT a braced frame. It is not a chevron braced frame. It is essentially a moment frame.

You would assume all the joints are pinned. Solve for the reactions, by either assuming they are equal or by the method suggested by BAretired. Once you have both reactions, the system is determinant and you can solve by basic FBD.

 

[KootK]

Took a similar approach in this thread this morning, including the FBD.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[BAretired]

The reason I don't want to assume a roller, in order to make this a determinate system, is that I want to be able to apply any loading scenario to this braced frame in either direction. It seems like we all agree that the first sketch is stable and indeterminate to the 1st degree.

Assuming a roller at one of the supports does not prevent you from applying any loading scenario in either direction.

Regarding the second sketch, Since the kicker is attached "at the pin", I see the number of force reactions at this location as 2. However, that would sum the total number of force reactions as 10 (2 at pinned base, 2 at pinned base, 2 at corner, 2 at corner, 1 at kicker to beam gusset, 1 at kicker beam gusset. This is compared to 11 equations of equilibrium, and is unstable by one degree. However, looking at sketch 2 it logically seems stable. This braces frame is almost categorized as truss since each member is pin connected at its ends EXCEPT that the gusset is located at the beam mid span which requires us to use the r vs 3n rule (instead of b + r vs 2j).

By assuming the removal of one kicker to make the structure statically determinate, there is only one force involved, namely the compression in the kicker. Sketch 2 is no different in principle than Sketch 1.

When you design a chevron frame, do you assume fixed corners? How do you solve a chevron by hand?

I would assume the corners are hinged. Without the chevron brace, the structure is unstable, so all of the horizontal load goes into the chevron brace. If the beam has gravity load, each brace in Sketch 3 will be loaded in compression in the absence of any horizontal force.

BA

 

[Once20036]

"...knee-braced frame behaves as a moment frame..."
Sketch 1 is the knee braced frame. I agree that it behaves as a moment frame, but I would not call it a moment frame. I appreciate your reference to commentary AISC 341-10 E1.2.

"...Sketch #2 is NOT a braced frame. It is not a chevron braced frame. It is essentially a moment frame. "
I would design sketch 2 as an ordinary concentric braced frame, specifically, and inverted V braced frame. Refer to AISC 341-10 F.1.4a. The system does not rely on the flexure strength of any member for stability, so how can you call this a moment frame?