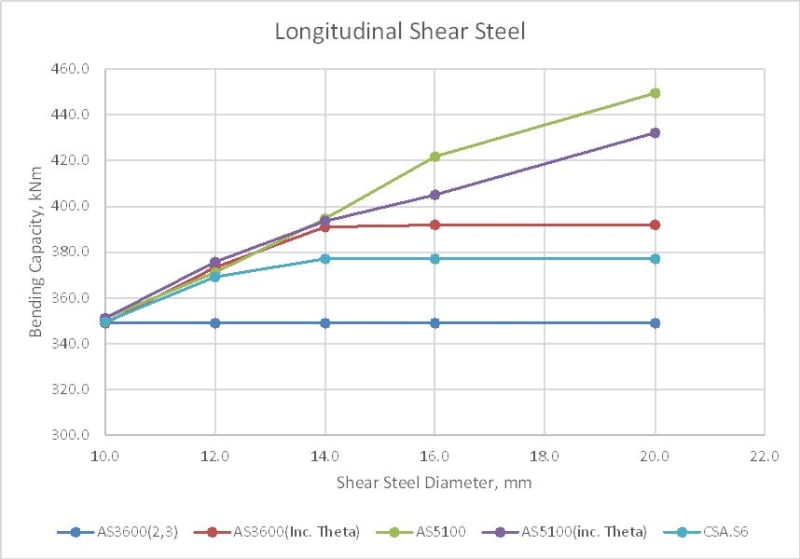
I have recently had a look at this amendment. This is now different from the same equation in AS 5100.5 as phiV_us has been replaced by (V* - phiV_uc), and "gamma_p P_v" by "0.5 gamma_p P_v". This equation is also different from those of AASHTO and the Canadian code. Does anyone know the reasons for these changes?
A potential problem arises if adopt this equation in AS5100.5, and use it for load rating to AS 5100.7.
When using (V* - phiV_uc) instead of phiV_us, there is an implicit assumption that the ligaments (stirrups) provided is such that phiV_us + phiV_uc > V*, which is okay for designing bridges. Section-shear deficient bridges have [phiV_us + phiV_uc] < V*, i.e., [V*-phiV_uc] > phiV_us. If we use the AS 3600 equation to load rate force in the longitudinal steel, this introduces inaccuracy as the amount of force deducted (V* - phiV_uc) is larger than phiV_us. The canadian code has a limit "V_s not to be taken great than V_u" for their equation which uses V_s.
A potential problem arises if adopt this equation in AS5100.5, and use it for load rating to AS 5100.7.
When using (V* - phiV_uc) instead of phiV_us, there is an implicit assumption that the ligaments (stirrups) provided is such that phiV_us + phiV_uc > V*, which is okay for designing bridges. Section-shear deficient bridges have [phiV_us + phiV_uc] < V*, i.e., [V*-phiV_uc] > phiV_us. If we use the AS 3600 equation to load rate force in the longitudinal steel, this introduces inaccuracy as the amount of force deducted (V* - phiV_uc) is larger than phiV_us. The canadian code has a limit "V_s not to be taken great than V_u" for their equation which uses V_s.