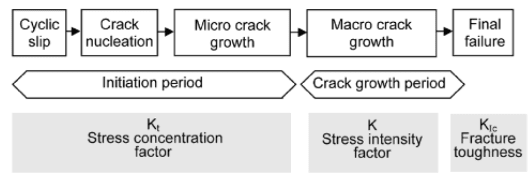
I have been trying to sort of distinguish between stress concentration factors and stress intensity factors. I have managed to write a bit.
Stress concentration factor tells you by what factor the local stress is higher than the far field/reference stress.
It is purely a geometry driven parameter (not dependent on the magnitude of applied stress although might depend on the kind of loading (axial, bi-axial, shear etc), allowable stress or anything else ..just pure geometry). Based on Kt alone you cannot say much about the health of the structure in any quantitative manner. You can have a Kt=10 and still be OK cause your max. applied stress is low enough to allow for such high Kts. (Yes, it will not be a great design, but you will survive).
Also, concept of Kt itself is null and void if you have a crack where the crack tip has sharp notch with near zero radius. You will get a theoretical Kt of infinity at that crack tip based on which you will predict that your local stress is infinite any non-zero applied stress and that your structure will fail. But experience showed that just because you predicted infinite local stress, the structures in practice didn't fail. And that's where the concept of stress intensity factor(SIF) comes in.
Stress intensity factor takes into account three things.1) the applied stress 2) geometry 3) crack length. If your applied stress goes up, your SIF goes up. You make the geometry mess, SIF goes up. You increase the crack length, SIF goes up. SIF provides you with a way of quantifying the state of stress around the crack. If you do not have a crack, your stress intensity factor is 0 but your stress concentration factor will still be the same old. The stress intensity factor sort of provides you with a single number which sort of wraps everything you are concerned into one. If two different structures have the same SIF, (although they may have different applied stresses, different geometries and different crack lengths), those two structures have the same stress field under the given conditions of stress, geometry and crack length. Now having calculated the SIF, you can compare it with the critical stress intensity factor (Kcrit) to determine if your structure is OK or not. This Kcrit is the SIF at which you have a runaway crack and is akin to the traditional material allowable.
The figure attached is from a book by Jaap Schijve which essentially says that when the cracks are microscopic, (as in when there are "NO" cracks, the concept of Kt is applicable) but once a crack is formed the concept of Kt cease to be a meaningful one and you essentially transition to the stress intensity concept.
Is that a fair summary?
Stress concentration factor tells you by what factor the local stress is higher than the far field/reference stress.
It is purely a geometry driven parameter (not dependent on the magnitude of applied stress although might depend on the kind of loading (axial, bi-axial, shear etc), allowable stress or anything else ..just pure geometry). Based on Kt alone you cannot say much about the health of the structure in any quantitative manner. You can have a Kt=10 and still be OK cause your max. applied stress is low enough to allow for such high Kts. (Yes, it will not be a great design, but you will survive).
Also, concept of Kt itself is null and void if you have a crack where the crack tip has sharp notch with near zero radius. You will get a theoretical Kt of infinity at that crack tip based on which you will predict that your local stress is infinite any non-zero applied stress and that your structure will fail. But experience showed that just because you predicted infinite local stress, the structures in practice didn't fail. And that's where the concept of stress intensity factor(SIF) comes in.
Stress intensity factor takes into account three things.1) the applied stress 2) geometry 3) crack length. If your applied stress goes up, your SIF goes up. You make the geometry mess, SIF goes up. You increase the crack length, SIF goes up. SIF provides you with a way of quantifying the state of stress around the crack. If you do not have a crack, your stress intensity factor is 0 but your stress concentration factor will still be the same old. The stress intensity factor sort of provides you with a single number which sort of wraps everything you are concerned into one. If two different structures have the same SIF, (although they may have different applied stresses, different geometries and different crack lengths), those two structures have the same stress field under the given conditions of stress, geometry and crack length. Now having calculated the SIF, you can compare it with the critical stress intensity factor (Kcrit) to determine if your structure is OK or not. This Kcrit is the SIF at which you have a runaway crack and is akin to the traditional material allowable.
The figure attached is from a book by Jaap Schijve which essentially says that when the cracks are microscopic, (as in when there are "NO" cracks, the concept of Kt is applicable) but once a crack is formed the concept of Kt cease to be a meaningful one and you essentially transition to the stress intensity concept.
Is that a fair summary?