i am not sure which approach to take AISC 15 indeed says its not required to check for
shear yielding(plastification) and only to check for punching shear
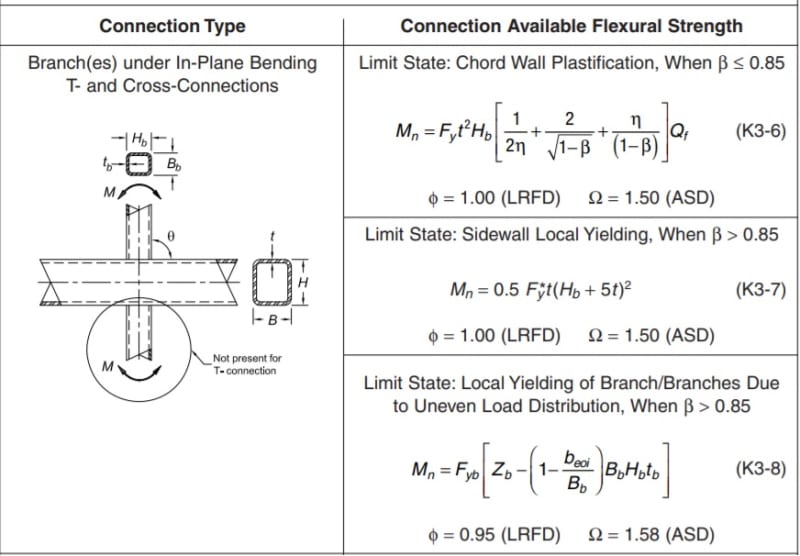
but i tried using the flexural strength for connection formula ( chord plastification) even though it says not applicable for β < 0.25
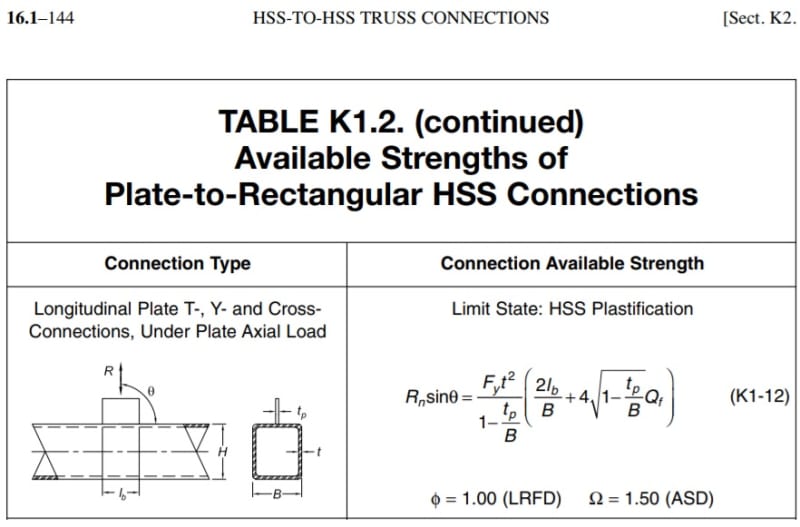
but it also says that for axial branch table K2.2 and they use the same equation for longitudinal plates
anyways for this example im getting higher ratios for chord plastification than punching
see sample calc below
Connection Loading:
Beam end Reaction (Shear), R = 11 kips
Member Properties:
Tab Yield Stress, Fyp = 36 ksi
Beam Tab Height, Hp = 8 in.
Tab Thickness, tp = 0.25 in.
Distance to row of bolts, D2 = 3 in.
Girder/column web thickness, twg = 0.25 in.
Girder/column width, B = 8 in.
weld thickness = 0.25 in.
Fyg - column/girder yield stress = 46 ksi
Fug- column/girder ultimate stress = 58 ksi
E = 29000 ksi
The available strength of the face of the HSS for the limit state of punching shear
Ω = 2
Ra * e = 33 kip-in.
Fu*t*lp^2/5= 93 kip-in.
Check Ra * e <= 1/Ω*Fu*t*Hp^2/5 AISC Manual Eq. 10-7a
Result Ra*e/(1/Ω*Fu*t*lp^2/5) 0.333333 < 1, O.K.
Connection available flexural strength table K3.2 chord plastification
lb = 8.00 in. lb = Hb/sinθ
η = 1.0 η = lb/B
β = 0.03125 β = Bb/B
did not use U and using Qf as 1 for this example (Qf really below 1 if using U so Mn even less)
Qf = 1 Qf = sqrt(1-U^2) Eqn K1-17
Mn = 54.65 kip-in. Mn = (1/1.5)*(Fy * t^2*Hb) * [ (1/(2* η)) + 2/sqrt(1-β) + (η/(1-β)) ]*Qf Eqn K3-6
Result Ra*e/Mn = 0.54839 < 1, O.K.