Why can't we use steel as Qing skin instead of aluminum alloy 2024.. although skin is lighter in weight when compared to aluminum alloy 2024.. density of steel is more than aluminum alloy.. is there any engineering reason ( tensile or compression ) other material properties to use aluminum alloy as wing skin ?
Tek-Tips is the largest IT community on the Internet today!
Members share and learn making Tek-Tips Forums the best source of peer-reviewed technical information on the Internet!
-
Congratulations JAE on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
Why can't we use steel as wing instead of aluminum alloy 11
- Thread starter MCA1983
- Start date
TugboatEng
Marine/Ocean
Space-X used a stainless steel skin for their rocket. I'm sure that could be adapted to a wing. Very high speed aircraft have used Inconel type alloys for regions that see high heating.
-
7
- #3
The most common material metrics are strength-to-weight (Ftu/rho) and stiffness-to-weight (E/rho). If you consider E/rho of aluminum, steel, and titanium, they all have about the same value, so there would appear to be little to choose. However, there are other metrics that are often more important, but less often discussed. For example, for column buckling, the metric is (E)^1/2 / rho and for plate buckling it is (E)^1/3 / rho. When you check either of these metrics, you find that aluminum scores higher than steel or titanium.
For an entire airframe, how much each failure mode governs the structural sizing must be considered. If your tensile strength is 10% better, but only 10% of the structure is sized by tensile strength, then your net weight savings due to improved tensile strength is only 1%. A large proportion of airframe weight consists of thin walled structures, which are often buckling critical, therefore the (E)^1/3 / rho metric may be the most representative.
The 1982 paper by Ekvall (see below) considers 7 failure modes, shows metrics for each, and divides the airframe weight into 7 zones governed by each failure mode to estimate weight savings with improved materials.
Finally, the above only considers mechanical properties, and of course there are many other factors to consider. Can you get the material you want tomorrow, or must you special order it and wait 6 months? Would it be worth a cost of 10 times more to save 10% weight? It may have better metrics, but have poor corrosion characteristics, would you use it?
The following references are worth consulting...
PAPER
"Methodology for evaluating weight savings from basic material properties" Ekvall, Rhodes, Wald, ASTM, 1982
BOOKS
Materials Selection in Mechanical Design, M. F. Ashby, 2005
Optimum Structural Design, Leonard Spunt, 1971
Weight-Strength Analysis of Aircraft Structures, F. R. Shanley, 1960
Minimum Weight Analysis of Compression Structures, G. Gerard, 1956
For an entire airframe, how much each failure mode governs the structural sizing must be considered. If your tensile strength is 10% better, but only 10% of the structure is sized by tensile strength, then your net weight savings due to improved tensile strength is only 1%. A large proportion of airframe weight consists of thin walled structures, which are often buckling critical, therefore the (E)^1/3 / rho metric may be the most representative.
The 1982 paper by Ekvall (see below) considers 7 failure modes, shows metrics for each, and divides the airframe weight into 7 zones governed by each failure mode to estimate weight savings with improved materials.
Finally, the above only considers mechanical properties, and of course there are many other factors to consider. Can you get the material you want tomorrow, or must you special order it and wait 6 months? Would it be worth a cost of 10 times more to save 10% weight? It may have better metrics, but have poor corrosion characteristics, would you use it?
The following references are worth consulting...
PAPER
"Methodology for evaluating weight savings from basic material properties" Ekvall, Rhodes, Wald, ASTM, 1982
BOOKS
Materials Selection in Mechanical Design, M. F. Ashby, 2005
Optimum Structural Design, Leonard Spunt, 1971
Weight-Strength Analysis of Aircraft Structures, F. R. Shanley, 1960
Minimum Weight Analysis of Compression Structures, G. Gerard, 1956
-
1
- #4
Wing skin needs to resist bending from pressure loads - bending resistance in that direction is resisted by depth of the material to the cube of the depth, while weight depends only on depth, both on a per width basis. For most metals stiffness is per weight (density). Aluminum ~ 1/3 density of steel, 1/3 modulus of steel, so a section 3X thick has a similar weight, 27 times the section, but 1/3 as stiff for a total 9X the stiffness at the same weight. Carbon fiber composites are even more advantageous, but the material has been much more costly, limiting past use. That has changed a lot.
For structures where the section is not limited to large, thin sheets, such as tubes used to make frames as is the case for fabric covered airplanes, steel dominates. And Russia used steel for wing skins on supersonic interceptors where aluminum would not survive the heat. Made the plane very heavy.
For structures where the section is not limited to large, thin sheets, such as tubes used to make frames as is the case for fabric covered airplanes, steel dominates. And Russia used steel for wing skins on supersonic interceptors where aluminum would not survive the heat. Made the plane very heavy.
- Thread starter
- #5
Ti may be an option for Al (not just 2024, also 7050/7075) ... except on cost.
"Black Aluminium" = Carbon composites tend to be option of choice.
search the full title ... STP288675 ... $25 from ASTM.
google found similar articles, more up to date, like ICAS 88.6.7.2 from an ICAO symposium.
"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.
"Black Aluminium" = Carbon composites tend to be option of choice.
search the full title ... STP288675 ... $25 from ASTM.
google found similar articles, more up to date, like ICAS 88.6.7.2 from an ICAO symposium.
"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.
SWComposites
Aerospace
What size airplane?
Wing design is typically highly complex. There are lift/drag goals, fuel volume goals, bending moments, torsional moment, flutter considerations, deflection constraints, local landing gear and control surface loads, damage tolerance considerations, and on and on - all of which have effects on sizing.
Wing design is typically highly complex. There are lift/drag goals, fuel volume goals, bending moments, torsional moment, flutter considerations, deflection constraints, local landing gear and control surface loads, damage tolerance considerations, and on and on - all of which have effects on sizing.
-
1
- #8
"Appendix C" of the following document is another source for the Ekvall methodology. I believe it is a publically available document via the DTIC technical reports website.
Development of Advanced Aluminum Alloys from Rapidly Solidified Powders for Aerospace Structural Applications, by R. E. Lewis, Lockheed Palo Alto Research Laboratory
(this is one in a series of progress reports with the same title, this one is dated March 1979)
It also appears in the Internet Archive:
Development of Advanced Aluminum Alloys from Rapidly Solidified Powders for Aerospace Structural Applications, by R. E. Lewis, Lockheed Palo Alto Research Laboratory
(this is one in a series of progress reports with the same title, this one is dated March 1979)
It also appears in the Internet Archive:
-
1
- #9
TugboatEng
Marine/Ocean
we can use steel, but it isnt economical. I had a client (with way too much money) who wanted to reskin a plane in Titanium (from Aluminium) ... 'cause it'd look cool ...
"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.
"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.
Compositepro
Chemical
The Pima air museum in Albuquerque is a fantastic place to visit, in the middle of the Air Force bone yard, and near the National Atomic Museum (
I think next time I drive to California in the spring that I will set aside a day for them.
I think next time I drive to California in the spring that I will set aside a day for them.
TugboatEng
Marine/Ocean
I'm visiting my wife's family in Tucson right now. I was scrolling through the aircraft list to kill time and clicked on that one because I had never heard of Budd. What a coincidence.
First Budd aircraft.
Budd made passenger trains, truck trailers, body stampings for automobiles and various other stuff.
They invented the spot welding method for stainless, which was useful for trains, not so much for aircraft.
Budd made passenger trains, truck trailers, body stampings for automobiles and various other stuff.
They invented the spot welding method for stainless, which was useful for trains, not so much for aircraft.
Seem to recall the V1 Buzz Bomb was made of thin steel and spot welded. Kept cost low and aluminum was a strategic material in short supply. A V1 cost less than 5% of what a V2 cost.
Not necessarily a good aircraft example as it only had to fly once for a few hundred miles.
Not necessarily a good aircraft example as it only had to fly once for a few hundred miles.
gibran_alves
New member
basically, weight.
steel has excellent mechanical properties, but is very heavy (high density); meanwhile an alluminum alloy has mechanical properties good enough to aeronautical use, but is very light.
steel has excellent mechanical properties, but is very heavy (high density); meanwhile an alluminum alloy has mechanical properties good enough to aeronautical use, but is very light.
-
1
- #18
Ohhhh... lots more reasons why alloy steel, stainless steel [SStl] [and Titanium, somewhat too], etc... are generally 'not suitable' for 99% of aircraft structures... and even launch-vehicle bodies... except for vehicles subjected to repeated high supersonic speeds/heating, etc...
I wish I had the time... here are few blivits...
difficult to form
Difficult 'strengthening' after forming without warping
difficult cutting/deburring/machining/drilling/fastening/welding etc with 'hard, tough, thin, etc materials [noted]'
Integral fuel tanks would be a bear to seal.
Specialized cutting tools required
Stl & SStl are very corrosion prone under certain circumstances!!
poor electrical grounding, bonding, conductivity, static electricity, etc...
high materials costs and availability
poor strength/weight, stiffness/weight
etc
xxxxxxxxxxxx
RB... for the life of me... I could not find any on-line reference to STP288675 / ASTM.
Regards, Wil Taylor
o Trust - But Verify!
o For those who believe, no proof is required; for those who cannot believe, no proof is possible. [variation, Stuart Chase]
o Unfortunately, in science what You 'believe' is irrelevant. ["Orion", HBA forum]
o Only fools and charlatans know everything and understand everything." -Anton Chekhov
I wish I had the time... here are few blivits...
difficult to form
Difficult 'strengthening' after forming without warping
difficult cutting/deburring/machining/drilling/fastening/welding etc with 'hard, tough, thin, etc materials [noted]'
Integral fuel tanks would be a bear to seal.
Specialized cutting tools required
Stl & SStl are very corrosion prone under certain circumstances!!
poor electrical grounding, bonding, conductivity, static electricity, etc...
high materials costs and availability
poor strength/weight, stiffness/weight
etc
xxxxxxxxxxxx
RB... for the life of me... I could not find any on-line reference to STP288675 / ASTM.
Regards, Wil Taylor
o Trust - But Verify!
o For those who believe, no proof is required; for those who cannot believe, no proof is possible. [variation, Stuart Chase]
o Unfortunately, in science what You 'believe' is irrelevant. ["Orion", HBA forum]
o Only fools and charlatans know everything and understand everything." -Anton Chekhov
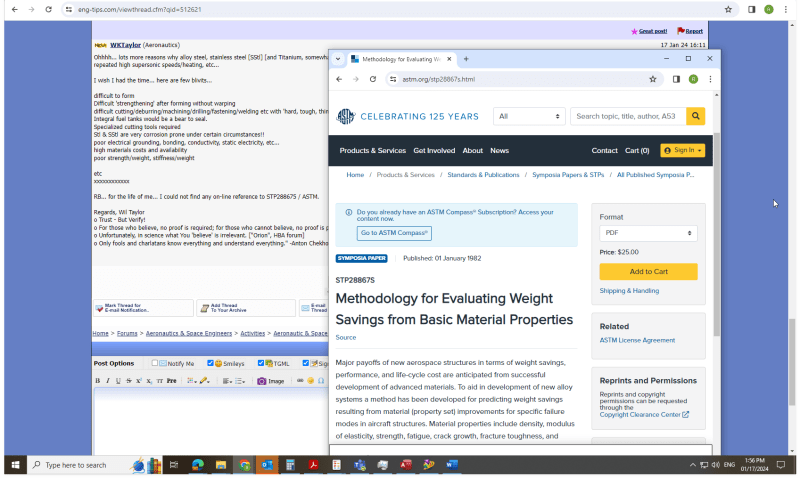
what I meant was ... search for the full title of Ekvall's paper "Methodology for evaluating weight savings from basic material properties".
screenshot attached shows the STP number (which my google couldn't find either !?, so I retraced my steps, again)
"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.
screenshot attached shows the STP number (which my google couldn't find either !?, so I retraced my steps, again)
"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.
- Status
Similar threads
- Locked
- Question
- Locked
- Question
- Question
- Locked
- Question