Two way shear stress - ACI property analoguous to polar moment of inertia 2

[canwesteng]

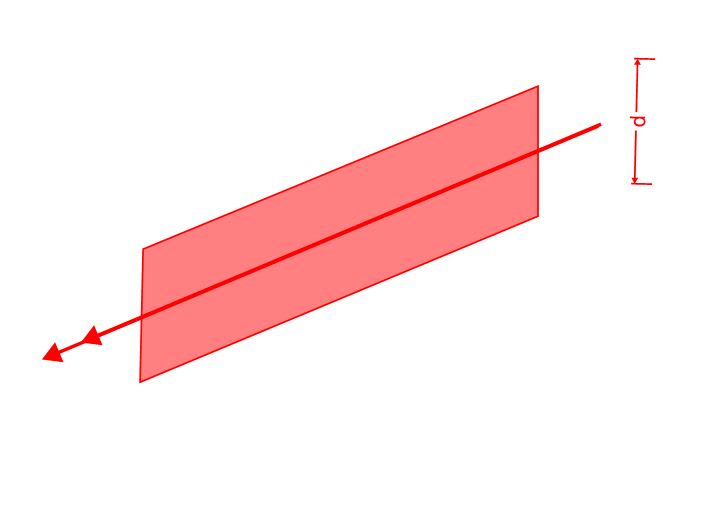
This is something that has been driving me nuts for some time, as I could never reconcile polar moment of inertia with the formula presented in the code. I've sketched out how I think it should work for a center and edge column, and I'm wondering if anyone agrees with me. Hope this is of some use to someone searching for this in the future as well.

 

[KootK]

We hit this issue pretty hard in your 2017 thread: Link. Was something left unresolved there? Basically it comes down to the d^3 terms being excluded because, while they make solid theoretical sense for an elastic, isotropic material, they don't fit well with concrete punching shear design for the reasons mentioned in the other thread.

 

[Settingsun]

That matches for the centre column case, but why is the middle term included? The one you tagged as I_y.

 

[canwesteng]

Nothing unresolved - I just came back to that, and wanted to sketch it out so my interpretation of it was more clear.

The middle term in ACI appears to be the "I.y" of line being considered, so I think it sticks around no matter what

 

[Settingsun]

But why is the I_y component relevant for uniaxial moment? What is its physical significance to the stress distribution?

 

[KootK]

Are you referring to a particular set of equations in an ACI document that we could check out?

I feel that it's worth noting that the resistance provided by the planes associated with the d^3 terms will often be neutered at ULS because they'll be flexurally cracked.

 

[canwesteng]

Well, neither the I.x or I.y components appear to have a physical significance to moment distribution, so I normally just ignored them when calculating J.

Unfortunately I'm just referring to the commentary in ACI 318 and trying to interpret what they mean by polar moment of inertia.

If you read this paper it seems to agree with the A*d^2 only method, but doesn't offer much more info.

https://www.concrete.org/publications/internationalconcreteabstractsportal.aspx?m=details&ID=19463

 

[KootK]

Are you just looking for the forumula derivations and/or confirmation of your own? I've got plenty of stuff but I don't want to bust out the dropbox scanner on my phone until I'm sure that I know what you're looking for.

 

[KootK]

One of the best treatments of this that I know of is in the book shown below. It's a killer book across the board as far as practical design goes and a used copy would probably be the best $24 CAD you ever spent.

 

[Settingsun]

I see what I missed on the side face. And the maximum stress in the corner from a usual polar calculation is ignored with the stress assumed constant (or averaged) over the depth.

 

[Agent666]

For what it's worth for comparison purposes, the author of this blog went through and derived all the common cases. Refer to the linked pdfs near the end of the post.

 

[canwesteng]

Thanks all, those are some good resources. I think my derivation ends up being the same as the blog