canwesteng
Structural
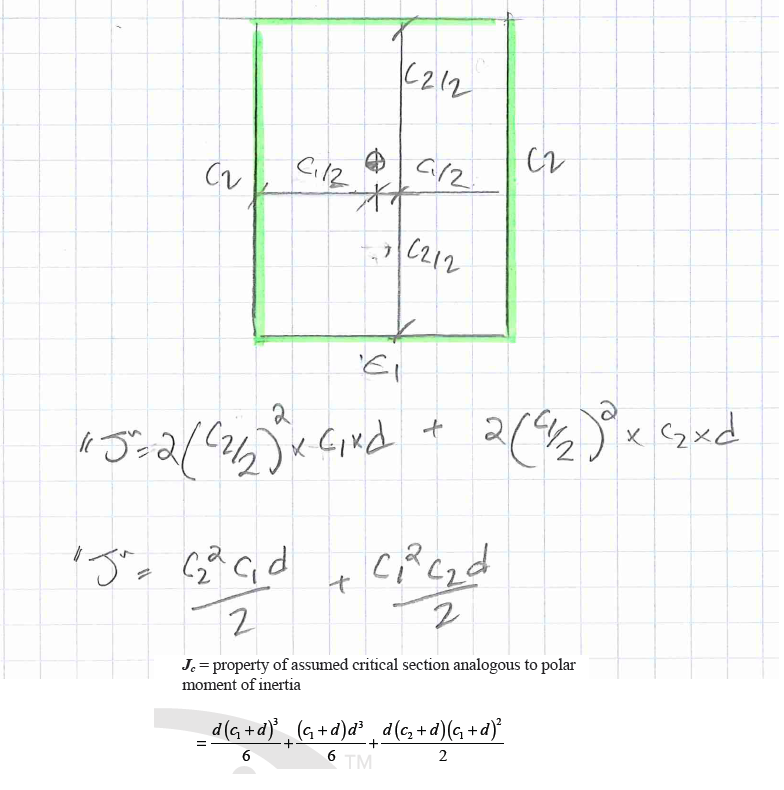
ACI 318 R8.4.4.2.3, and CSA 13.3.5.5 make reference to a property of the critical shear section that is called "analoguous to the polar moment of inertia". The polar moment of inertia should be the radial distance from centroid multiplied by an increment of area, integrated over the area.
I'm at an absolute loss as to how they've calculated the formulas they use to determine the polar moment of inertia for an interior column, and so can't create my own for the case of an exterior column, or a circular column. Can anyone shed some light on this?
I'm at an absolute loss as to how they've calculated the formulas they use to determine the polar moment of inertia for an interior column, and so can't create my own for the case of an exterior column, or a circular column. Can anyone shed some light on this?