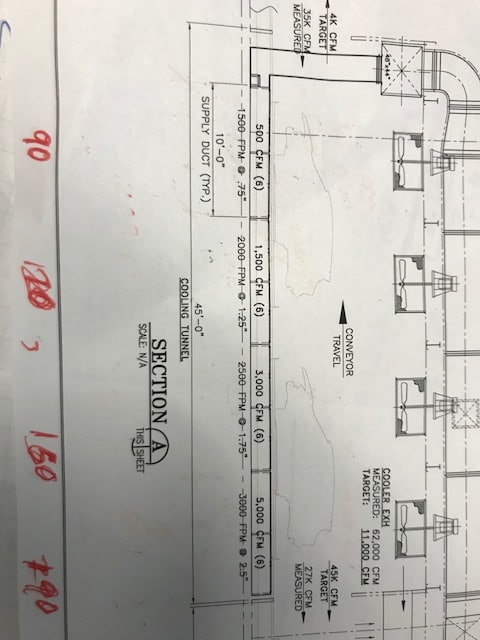
Here's a tough one.
A 334.69kg car body with a surface area of 113 m^2 exits a oven at 124 deg C. While the car is moving at .0366 m/s, 27 deg C air is forced toward the vehicle from the lower sides at 15.24 m/s from within .30 meters away. What is the new average temperature of the car body after 3 meters or 83 seconds.
My equation: I EITHER BLEW SOMETHING SOMEWHERE OR USED THE WRONG EQUATION.
Heat Transfer Coefficient hc=10.45-V+101/2 hc=34.25 W/(m2K)
Heat Transfer (q)
q=(hc)(area)((surface temp)-(air temp))
q=(34.25)(113)((124)-(27))
q=352,506 W
Tf= Ti + [q/(m*specific heat of steel)]
Tf=124 +[352,506/(334690 grams*.5108 J/(g-deg C)
deltaT=2.06 deg C
Tf=121.94 deg C
Tff = 121.94 - (2.06*83) = -49.04 deg C (WHICH OBVIOUSLY CANNOT BE THE NEW TEMP)
After the first 3M the vehicle continues to a second 3M section but the forced air velocity goes down to 12.7 m/s
A 334.69kg car body with a surface area of 113 m^2 exits a oven at 124 deg C. While the car is moving at .0366 m/s, 27 deg C air is forced toward the vehicle from the lower sides at 15.24 m/s from within .30 meters away. What is the new average temperature of the car body after 3 meters or 83 seconds.
My equation: I EITHER BLEW SOMETHING SOMEWHERE OR USED THE WRONG EQUATION.
Heat Transfer Coefficient hc=10.45-V+101/2 hc=34.25 W/(m2K)
Heat Transfer (q)
q=(hc)(area)((surface temp)-(air temp))
q=(34.25)(113)((124)-(27))
q=352,506 W
Tf= Ti + [q/(m*specific heat of steel)]
Tf=124 +[352,506/(334690 grams*.5108 J/(g-deg C)
deltaT=2.06 deg C
Tf=121.94 deg C
Tff = 121.94 - (2.06*83) = -49.04 deg C (WHICH OBVIOUSLY CANNOT BE THE NEW TEMP)
After the first 3M the vehicle continues to a second 3M section but the forced air velocity goes down to 12.7 m/s