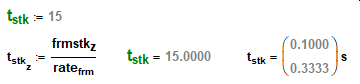These are some personal likes about Mathcad. I hope they give you some ideas into your software development.
In my engineering experience, I've mainly used Mathcad. The first thing I like about it is that it is a 'blank sheet'. That permits the user to display their work in whatever type of format they prefer, from the 'quick pencil scribble' to the full blown 'Engineering Documentation Justification Report'. That's what I like, the flexibility. In my case, I go for the Report format. The visual 'Word Processing' capabilities can make the pages look very professional.
I'm keen on the units. I've been asked to check peoples work, where they haven't used units (be it Mathcad or Excel). In the case of Mathcad, units is like a check, if your accidentally working with mixed units, it lets you know!
Graphing, in 2D and 3D. This has come in handy! 3D has helped in things like plotting rectangular plate displacements, stress fields, 3D bolt groups, etc.
Being able to write out an equation, with variables that haven't been defined has helped.
Example would be p(x,y,k,u.v) = k.sin(pi.u.x/b).cos(pi.v.y/a), for use such as in min. potential energy methods!
Also the general solution, y(x,A,B,P) = A.cos(k(P).x) + B.sin(k(P).x), for use in things like beam column deflection & buckling.
This then permits the equation to be used in a 'solve block', where unknowns can be solved (linear and non-linear solvers) by equating to known boundary / loading conditions etc within the 'solve block'. Use of 'solve blocks' has helped out tremendously!
Another aspect of Mathcad that has proven to be very handy is the integration and differentiation capabilities! For example, these capabilities have come in very useful for beam deflection calculations. Combined with the use of undefined variables (unknown variables to be found) and a 'solve block', numerous boundary conditions (transnational / rotational), differing materials (combination of components) and changing cross sections (stepped / tapered) along the beam, and loading combinations [distributed (linear / tapered / sinusoidal) / point loads / step moments] have been easily solved! Being able to symbolically solve these types of equations (integrals / differential) is also very useful! In some instances, the symbolically solved equations can be used instead of the built in integration / differentiation capabilities, thus speeding up the solution time.
For diagrams, including things like FBD, to aid in explaining methods etc, I like the ability to insert a picture, such as ‘Paint’, and be able to edit it.
Hope this helps.