stresses in framed structures

[chthulu]

Hi,
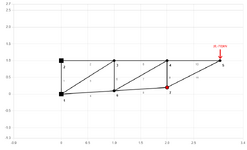
In the picture that follows, is fig 9 correct?
Using the scale in pounds shown there, the 70LBS line seems to be correct, where line a seems to be more or less 110 lbs and line b seems to be more or less 130 lbs, but using trigonometry I got something else for a and b.
So, is it possible to get a and b through trigonometry?
If you draw the line for the 70lbs according to the scale in pounds, how do you know where to stop when drawing a? or b? if you start from b.
I mean line a could be any length and fig 8 does not indicate how long line a should be.
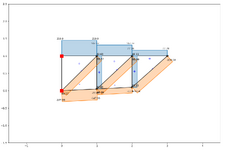
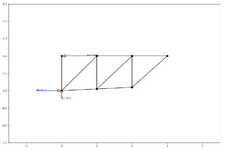
What would be the best way to add the sketch of fig 8 together?
I really do not understand even how the 180 and 230 lbs are get.

 

[WKTaylor]

Where did this figure come from? Bruhn?

 

[chthulu]

no, how-to-build-ultralights-amp-plans-by-herbert-beaujon

 

[WKTaylor]

More info is likely available at www.homebuiltairplanes.com/forums/...

How to Build Ultralights by Herbert Beaujon Technical Manual

Technical manual on How to Build Ultralights by Herbert Beaujon

www.homebuiltairplanes.com

Your 'worked/partially intact figure' came from pg. 24... this left me scratching my head.



There is a 'CAUTION' about using Beaujon's manual for design, posted in the following thread on the Hombuiltairplane.com/forums...

Herbert Beaujon- My all time hero !

Home or this specific page Tubing Connections I was bouncing around the internet and was happy to find a website that is sharing his work. He wasnt the most accomplished engineer ( was a real estate agent ) but he had the best imagination and was willing to put ideas on paper far...

www.homebuiltairplanes.com

 

[chthulu]

I can not read that post, since they changed the forum and made it private, I not going to give them money.

Anyway the caution most probably has nothing to do with what I asked.

 

[GregLocock]

I'd be very wary of using a reference that labels a force diagram as a stress diagram.

Anyway he's constructed a Cremona/Maxwell diagram . This is good. I'm not crazy about his notation, should have used Bow's.

The key to determining the forces in a and b is shown in the little triangle at the top right. The vertical component of 70 lbf can only be provided by b, which then generates a tension in a to react the horizontal component of b.

The force in each member is purely axial, hence must be aligned with the geometry of that member.

 

[rb1957]

I don't know this method, but the load in the rightmost member "b" is not 70 lbs, it's vertical component is.
I don't get the stress diagram from the truss geometry ... to show the load is member "a" at the left side of the stress/load graphic just seems so "wrong" (or certainly non-intuitive).

The reaction at A (and so at B too) is easily calculated (moments about B). The vertical reaction at B is 70 lbs.

Sure you can use force polygons, and so solve each joint. but the math to do this isn't hard.

Old methods like this are not gospel, they were developed a long time ago when tools we have (like excel and trig) were not so easy to use.
Sure, there is a place for them, but I would learn them as an adjunct to modern methods rather than as the way to solve a problem.

 

[WKTaylor]

Sorry... guys about HBA reference... I've been a member 'forever'... here are some excerpts...

Home or this specific page
Tubing Connections I was bouncing around the internet and was happy to find a website that is sharing his work. He wasnt the most accomplished engineer ( was a real estate agent ) but he had the best imagination
and was willing to put ideas on paper far ahead of people doing anything similar.
Apparently they are publishing/sharing his book "How to Build Ultralights."
I talked to him a few decades ago and he said he spent hundreds of hours
in libraries doing the research for his book. Flipping through his paper napkin
design ideas made me feel like a kid again. With todays technology and materials more and more of his ideas should be doable.
----------------------

I haven't stayed in a Holiday Inn in a really long time, but my advice is to approach that stuff on that tubing connections page with extreme caution. No doubt it could work for a shade canopy in your back yard, but I wouldn't trust it in an a/c.
ex: the eyebolt example loads the through-bolt in bending; tension on the eyebolt will eventually fail the through-bolt.
ex: there's a long, ongoing thread on this site right now about how difficult it is to bond anything to aluminum for actual structure

Perhaps the a/c he designed presented such low loads on the joints that there was never a failure, but if true, it would seem to indicate that the structure was heavier than needed.
----------------------

RVCharlie is completely right. Herbert was a real estate agent with imagination. You should not take ANYTHING he says as authoritative.... I dont however think that it is a mistake to follow his thinking as possible alternatives that could prove to be good or bad. He wrote about ultralights before people were building them and in that regard he was visionary in my opinion and he made attempts to research and qualify ... but question everything you read. Indeed a lot of his
suggestions are more hardware store type solutions for farm implements and yes they will definitely be heavier than possible but also usually cheaper and simple. Think WeedHopper.
An eyebolt solution can sometimes be acceptable as like anything else you design to a load plus some cushion for safety etc and add a little more for good measure and maybe you added some weight and saved some time and maybe money. You are the designer now. I just wanted to share Beaujon' s work as entertainment.
xxxxxxxxxxxxxxxxxxx

I have attached the Beaujon 'design document'... he is deceased. CAUTION... lots of sketchy info.

 

[chthulu]

Thanks, I got that pdf, but I was puzzled by that page, since I could not find anything like that about a fuselage.

 

[chthulu]

Now I used the online truss calculator and I got different results: (The default for the calculator is kN)

 

[rb1957]

can you show dimensions ? length is easy to deduce, I calculate pt7 at (2, 0.1) ?

when you're learning these methods, I'd suggest simplifying the structure (like make the lower chord parallel with the upper, use regular bay widths, ...);
then tweek these simpler models to get what you really want.

 

[chthulu]

what dimensions? there are no dimensions. Look at the picture at the top, it is all based on Cremona/Maxwell diagram, so no dimensions. However, I realized that when I used the online truss calculator, I should have put the same dimensions as fig. 9, that means printing the page and then check all the dimensions I get from fig. 9 with a ruler.

 

[GregLocock]

Eyeballing it the right hand triangle, b is roughly 2^.5*70, and a is roughly 70. Yes changing the dimensions will change the forces in the members.

 

[rb1957]

how did you make your FEM without dimensions ? (how do you make the structure without dimensions ??)

to my mind, this is a much more difficult way yo solve the truss, relying on accurate drafting (not my wheelhouse)

but each joint is solvable, starting at 5 you know the three directions and the size of one load, therefore you can draw any size of triangle and the other two sides are just linear factors of the known side. Then go to joint 7, then 4, etc ... at each joint you know the directions and one value, so you can scale for the other two.

Easier for me to use trig,

 

[chthulu]

Picture at the top fig. 8, no dimensions, which says:

Given: The truss shown above with an end load of 70 lbs.
Find: The tension load acting at point A. The compression loads acting at point B.

Compression loads act into a joint. Tension loads act away from joint. Starting at junction 1, fig. 8, form a force triangle as indicated by small sketch shown immediately above. Always measure load directions clockwise. Using the scale shown, mark a vertical distance of 70 lbs. in fig. 9. Your force triangle at 1, fig. 8, is drawn in fig. 9 as the force triangle shown by lines 70 lbs, a, and b. Junction 2, fig. 8, is drawn in fig. 9 as the farce triangle b, c, f. Follow through, remembering that no single force may be extended beyond itself. All your graphic forces 1 2,3,4 5, should fit together to form the complete force frame in fig. 9. The tension at A, fig. 8, is equal to the measured length of line h, fig. 9, or 230 lbs. By the same token, the compression loads at Bare 70 lbs. and 180 lbs. (1, j)

So let's forget everything else, how do you start from fig. 8 and end up with fig. 9?

Does anyone have experience with the Cremona/Maxwell diagram?

It is easy to draw the vertical line of 70LBS after you choose a scale like fig. 9, but how do you choose how long line a to start from, should be?

 

[rb1957]

do you realise that fig 9 even though it looks like fig 8, is the reverse of fig 8 ?

follow the text description, you start fig 9 with a vertical line representing the load, and know the direction of the other loads (horizontal and inclined) and you draw lines to represent these in a manner to create a closed triangle (so there are two ways to do this, one looks like fig 8; probably the text tells you which to construct). The length of these lines are the loads in these members, scaled from the 70 lbs line. You then solve joint 2 (with the inclined line above a vertical line, and a slightly inclined line) .... and repeat ...

 

[chthulu]

I guess you do not anything about how the Cremona/Maxwell diagram works.
Yes fig. 9 is as you said, but made in scale according the the scale provided.
No, it does not work as you says, the triangle 70lbs,a,b in fig. 9 represents the triangle a,b,c but according to a scale, now it is simple to draw the 70lbs according to the scale, but for a and b is a different matter, a and b are not give as lbs, so you can not use the scale to draw them, and you can not draw as you said line a as you please, because you do not know where to end it, there is no correspondence between the two triangles of fig. 8 and fig. 9.
The only way to get a right is using trigonometry and therefore knowing angle between c and b or a and b in fig. 8
All the rest is speculation.

 

[rb1957]

yep, I've never heard of "Cremona/Maxwell" diagrams, but I know how to solve a joint, graphically.

it does work as I say, 'cause what I say is the same as the text provided.

start with a vertical line that represents 70 lbs, doesn't matter how long it is, this sets up the scaling.
from one end (the upper) draw a horizontal line, from the other draw an inclined line representing member 1-2 in fig 8, so that it crosses the horizontal line.
the horizontal line represents the load in 1-3, and the load in 1-3 is this length divided by the length of your 70 lbs line (* 70 lbs)
and the inclined line is 1-2, and the load from the length a per above.
and repeat.

 

[chthulu]

You don't even read what I say, I said that is easy for the 70lbs line, the inclined line is not possible because you do not know how inclined the line should be, you can not approximate, you could incline the line as you please but will never be sure if it is inclined at the right angle unless you know one of the angles I mentioned. This is not something you can play with.

 

[rb1957]

it is inclined as it is in fig 8 ... the direction of the member in fig 8 is the direction of the load in fig 9 ...
this is what the method shows ... detail views of the joints show the directions of the individual loads which combine together to make a closed shape (or a force polygon).