This thread has been inspired by the practical issues posed in this other thread:
The issue was basically that Pf, or Pof = Probability of failure, sometimes, or often, seems to be high in relation to the FS, the minimum Factor of safety of the slope.
One possible reason: the soil properties are known not to be constant across the volumes of interest in geotechnical engineering. They exhibit statistical variations which have been studied by the theory of the random fields, first proposed by Vanmarcke.
The scale of fluctuation or SOF describes the autocorrelation of soil properties, that is, if the fluctuations are of high or low frequency, in other words, if there are small volumes of alternating weaker and stronger soil or relatively larger volumes of alternating weaker and stronger soil.
An example of a random field model in a slope is the following, from Mohammad Tabarroki; Fauziah Ahmad; Roodabeh Banaki; Sanjay K. Jha, JGGE ASCE 2013.
The first illustration is small SOF, the second illustration is large SOF, here it is well visible that elementary soil volumes tend to cluster in weaker and stronger areas.

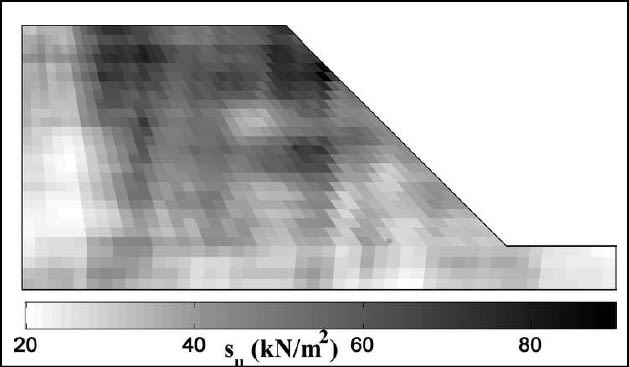
Now, a potential slip surface will cross thru weaker and stronger fluctuations.
IF the SOF is small (figure #1), any slip surface will most probably cross thru many weaker and stronger volumes of soil, so the average strength will always govern the stability.
If the SOF is large (figure #2), the scale of the slip surface is relevant. If the scale is such that the sliding surface will cross thru weaker and larger volumes (large sliding surface relative to the dimension of the fluctuation), than the average strength governs failure.
If the dimension of the sliding surface is potentially equal to or smaller than the dimension of the fluctuation, then the surface may be randomly contained in a weaker fluctuation. In this case, it is not the average strength that governs, but rather the average strength within the weaker volumes of soil.
IN SLOPE STABILITY USUALLY THE SLIDING SURFACE IS LARGER THAN THE SCALE OF THE FLUCTUATIONS, SO THE AVERAGE STRENGTH OF THE SOIL GOVERNS.
The above means that, in probabilistic analyses, the strength parameters should be represented not by the statistical distribution of the sample, but rather by the statistical distribution of the mean of the strength parameter. This may constitute a substantial difference since often the distribution of the mean has a much lower variability than the distribution of the sample. This results in a FOS distribution with a lesser variability hence, for a given average FOS>1, a lesser probability of failure (POF), that is a lesser probability that FOS<1.
The final result, if we adopt the distribution of the sample, is often an overestimation of POF.
(to be continued)
The issue was basically that Pf, or Pof = Probability of failure, sometimes, or often, seems to be high in relation to the FS, the minimum Factor of safety of the slope.
One possible reason: the soil properties are known not to be constant across the volumes of interest in geotechnical engineering. They exhibit statistical variations which have been studied by the theory of the random fields, first proposed by Vanmarcke.
The scale of fluctuation or SOF describes the autocorrelation of soil properties, that is, if the fluctuations are of high or low frequency, in other words, if there are small volumes of alternating weaker and stronger soil or relatively larger volumes of alternating weaker and stronger soil.
An example of a random field model in a slope is the following, from Mohammad Tabarroki; Fauziah Ahmad; Roodabeh Banaki; Sanjay K. Jha, JGGE ASCE 2013.
The first illustration is small SOF, the second illustration is large SOF, here it is well visible that elementary soil volumes tend to cluster in weaker and stronger areas.


Now, a potential slip surface will cross thru weaker and stronger fluctuations.
IF the SOF is small (figure #1), any slip surface will most probably cross thru many weaker and stronger volumes of soil, so the average strength will always govern the stability.
If the SOF is large (figure #2), the scale of the slip surface is relevant. If the scale is such that the sliding surface will cross thru weaker and larger volumes (large sliding surface relative to the dimension of the fluctuation), than the average strength governs failure.
If the dimension of the sliding surface is potentially equal to or smaller than the dimension of the fluctuation, then the surface may be randomly contained in a weaker fluctuation. In this case, it is not the average strength that governs, but rather the average strength within the weaker volumes of soil.
IN SLOPE STABILITY USUALLY THE SLIDING SURFACE IS LARGER THAN THE SCALE OF THE FLUCTUATIONS, SO THE AVERAGE STRENGTH OF THE SOIL GOVERNS.
The above means that, in probabilistic analyses, the strength parameters should be represented not by the statistical distribution of the sample, but rather by the statistical distribution of the mean of the strength parameter. This may constitute a substantial difference since often the distribution of the mean has a much lower variability than the distribution of the sample. This results in a FOS distribution with a lesser variability hence, for a given average FOS>1, a lesser probability of failure (POF), that is a lesser probability that FOS<1.
The final result, if we adopt the distribution of the sample, is often an overestimation of POF.
(to be continued)

