Simple yield line question

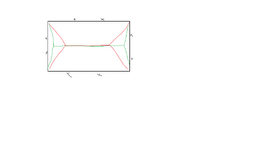
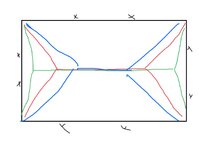
[canwesteng]

I'm having a brain fart here, and no one in my office is terrific with yield lines. Normally I take the yield line mechanism of a flat plate (fixed support in this case) to be the red line, with the diagonals at 45 degrees. However, the project length about the horizontal of the diagonal yield lines decreases the steeper they get and the vertical projection doesn't change. So the steeper these get the weaker the mechanism, though this seems irrational. It is simple to just call the diagonals 45 degrees in the case of reinforcement equal in each direction, but in this case the short side has less reinforcement than the strong side, so it must be somewhat steeper than 45. Is there something I'm missing?

 

[HS_PA_PE]

What is the geometry of the loading you're considering on the plate?

 

[canwesteng]

Just uniform loading for now

 

[HS_PA_PE]

Okay, I see.
I believe that the ratio of the reinforcement amounts in each direction would result in some ideal selection of the yield line pattern, with a steeper angle than the 45 deg., as you suggest. But as the length of the diagonal line projections continues to reduce, the angle of yielding along those diagonals increases, thus increasing the work required and strengthening the mechanism. At some point these should balance out.
... I'll see if I can find time to work an example. I'm a bit puzzled now myself.

 

[canwesteng]

I ended up working it out - you do end up with more yield line in total as the diagonals extend, but the work ends up being UDL x area x delta/3, and in the area that is a rectangular instead of a triangular, the work is UDL x area x delta/2. So more yield lines with the triangle but less work expended as they drift, which ends up getting to an equilibrium point.

 

[Tomfh]

Goes more to blue?

 

[canwesteng]

In my case specifically, more to the green and also up (negative moment resistance stronger at the bottom).

 

[Tomfh]

Goes to green? So you have more reo in short span?

 

[canwesteng]

Correct

 

[Tomfh]

Ok. green makes sense then. I had thought you had more bars in the long directions…

 

[271828]

Can't assume 45 deg or any other angle. YLA is an upper bound solution, so you'll need to find the angle that results in the lowest strength.

 

[canwesteng]

Well in an isotropic material, the yield lines will be symmetric, and if the supports are symmteric, you'll just end up with 45 degree angles.

 

[BAretired]

The only place I use yield line theory is for steel plates. For concrete slabs, I prefer the Hillerborg strip method.

For a steel plate, the capacity of the plate is equal in all directions, so m = Z*Fy where m is the yield strength of the plate per unit length in any direction, Z is the unit plastic modulus and Fy is the yield strength of the material. The coordinates of the yield line can be found by differentiating the expression for internal work, then selecting the coordinates which produce the most critical value.

 

[EngDM]

The only place I use yield line theory is for steel plates. For concrete slabs, I prefer the Hillerborg strip method.

For a steel plate, the capacity of the plate is equal in all directions, so m = Z*Fy where m is the yield strength of the plate per unit length in any direction, Z is the unit plastic modulus and Fy is the yield strength of the material. The coordinates of the yield line can be found by differentiating the expression for internal work, then selecting the coordinates which produce the most critical value.

Waht is your go-to reference for learning/worked examples for this? No one in my office uses yield line theory, but it's something I'd like to learn.

 

[canwesteng]

I recommend Practical Yield Line Design by Kennedy and Goodchild, you can probably find it online for free. I've never heard of BA's method of differentiating the equations for work or energy - I just plug the formulas into mathcad and iterate the inputs til I'm happy.