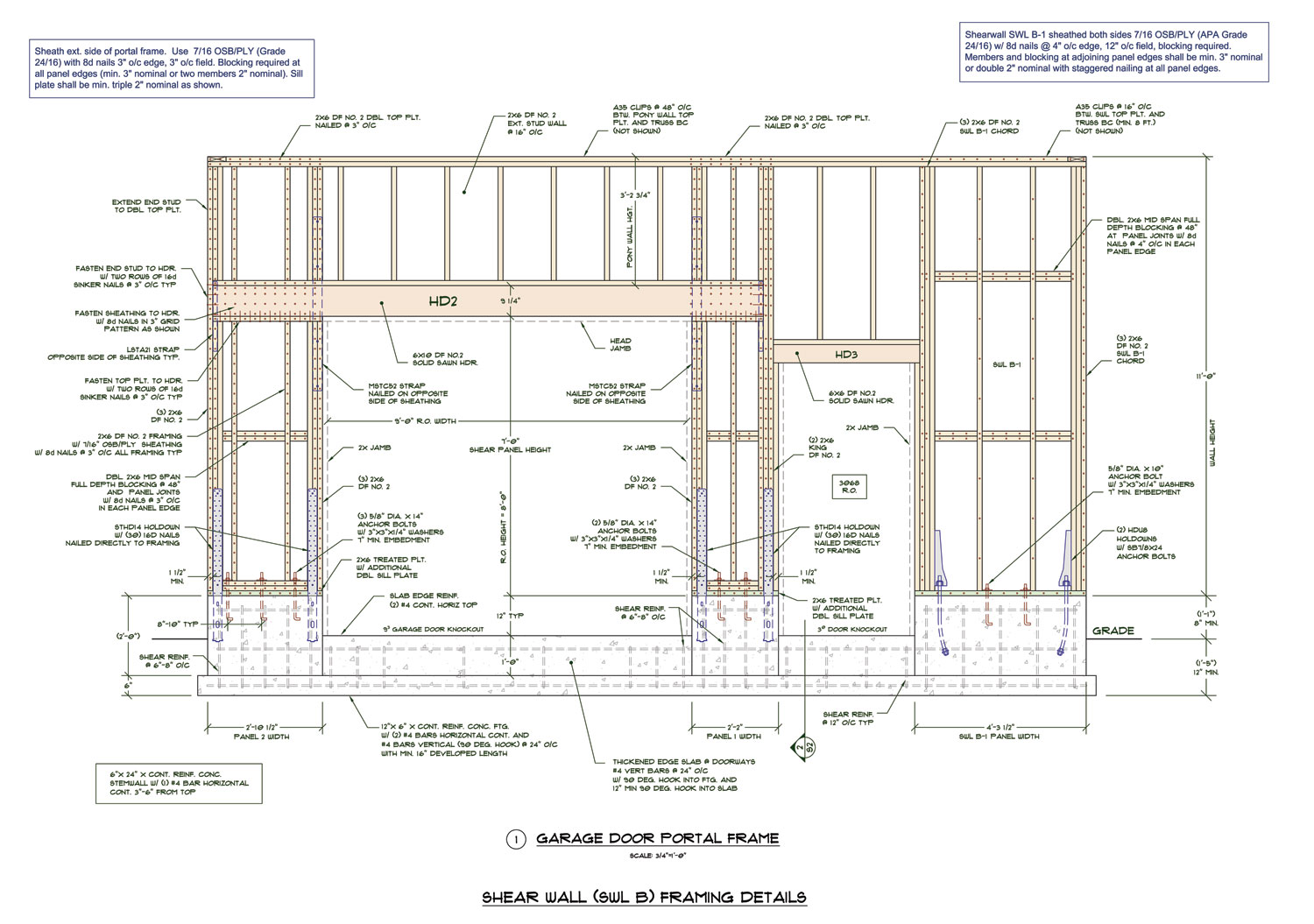
My previous analysis or attempts thereof of a typical wood portal frame assumes that the holdowns at the foundation and the moment connection of the nail grid into the header (and strap) more or less share the moment load equally and I basically give it a pass provided the combined capacity exceeds the actual load. See page 5 of previous analysis below:

However, is this assumption correct? or perhaps close enough?
My most recent spreadsheet for portal frames so far does not take into account the moment capacity of the nail gird, straps and sheathing. It essentially treats the pony wall and shear panels on each side of the opening as separate (segmented) shear walls, see below:
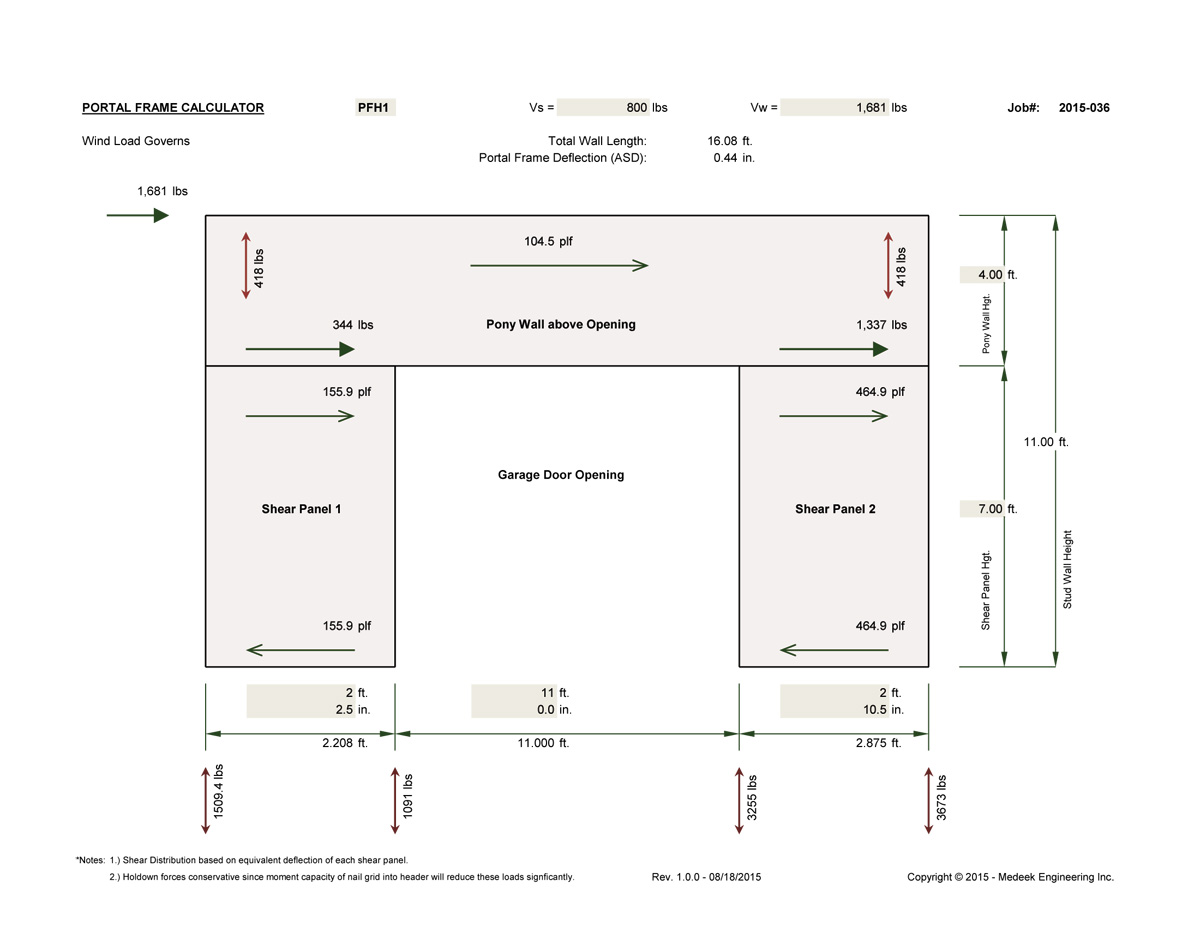
When the two legs of the double portal frame are different lengths I utilize the three term deflection equation from the SDPWS to compute the shear force to each leg such that the deflections are equal.
The problem I see with my current attempt at an analysis is that the holdown forces will actually be significantly less than shown since the moment connection at the shear panel/header interface (nail grid and strap) will decreases these forces at the foundation. The question is how do I quantify this decrease in holdown forces without an elaborate FEA model. I'm wondering if anyone has done this sort of thing before and might have some hints or ideas.
The other thought that came to me is the moment connection at the top of the shear panels will make the entire portal frame stiffer and hence decrease deflection as well as make it attract more load in a rigid diaphragm analysis.
A copy of my spreadsheet is located here is anyone is interested in looking at my algorithm for computing the deflection and the distribution of shear.
I actually started with the 4 term deflection equation but I could not get it to give reasonable answers when the difference between the two legs was only slightly different. I think it may have something to do with the non-linearity of the equation and the nail slip term.
A confused student is a good student.
Nathaniel P. Wilkerson, PE

However, is this assumption correct? or perhaps close enough?
My most recent spreadsheet for portal frames so far does not take into account the moment capacity of the nail gird, straps and sheathing. It essentially treats the pony wall and shear panels on each side of the opening as separate (segmented) shear walls, see below:

When the two legs of the double portal frame are different lengths I utilize the three term deflection equation from the SDPWS to compute the shear force to each leg such that the deflections are equal.
The problem I see with my current attempt at an analysis is that the holdown forces will actually be significantly less than shown since the moment connection at the shear panel/header interface (nail grid and strap) will decreases these forces at the foundation. The question is how do I quantify this decrease in holdown forces without an elaborate FEA model. I'm wondering if anyone has done this sort of thing before and might have some hints or ideas.
The other thought that came to me is the moment connection at the top of the shear panels will make the entire portal frame stiffer and hence decrease deflection as well as make it attract more load in a rigid diaphragm analysis.
A copy of my spreadsheet is located here is anyone is interested in looking at my algorithm for computing the deflection and the distribution of shear.
I actually started with the 4 term deflection equation but I could not get it to give reasonable answers when the difference between the two legs was only slightly different. I think it may have something to do with the non-linearity of the equation and the nail slip term.
A confused student is a good student.
Nathaniel P. Wilkerson, PE