I want to check we're comparing to the correct AISC capacity. In Celt83's post of 13 Nov 22:59, the grey box says Iy=52.7 which is the exact same number as the line above it for h/tw and about half of the actual Iy. Or does AISC use the I value for one flange? Not sure whether this value was carried into the calculations and it only makes ~6% difference in AS4100 anyway.
And, if we're trying to see whether AS4100 is dangerously unconservative, perhaps Yura's value of Cb should be used which is 3.67 for double-inflection segments compared with 1.923 from Celt83's calculation: 91% increase. Yura's would be unconservative in this case since it came from distributed loading rather than concentrated, but the stock AISC capacity seems certainly too low. Perhaps we should repeat the trial problem with distributed loading and the appropriate ratio of end:midspan moment to have the inflection points at the quarter points. Then Yura's Cb could be used directly.
Edit: Inflection at the quarter points gives Cb=2.78 according to Yura which should be closer to the mark. Increase of 44% over stock AISC.
Regarding the discussion of Kl=1.0 for top flange loading from 14 Nov 16:40 to 19:30, I thought the lateral restraint at the load location removes the tendency of the additional ('p-delta') torque to exacerbate the twist and promote instability. By being sufficiently stiff to qualify as a lateral restraint, it provides sufficient horizontal force above the shear centre to counteract the destabilising torque. Possible alternative view: the lateral restraint moves the point of rotation very close to the top flange and the vertical load has ~zero lever arm about the point of rotation despite the shear centre kicking sideways relative to the top flange.
KootK said:
AS4100 LTB capacities come out high relative to AISC. They're not high because they're wrong; they're high because they're more right.
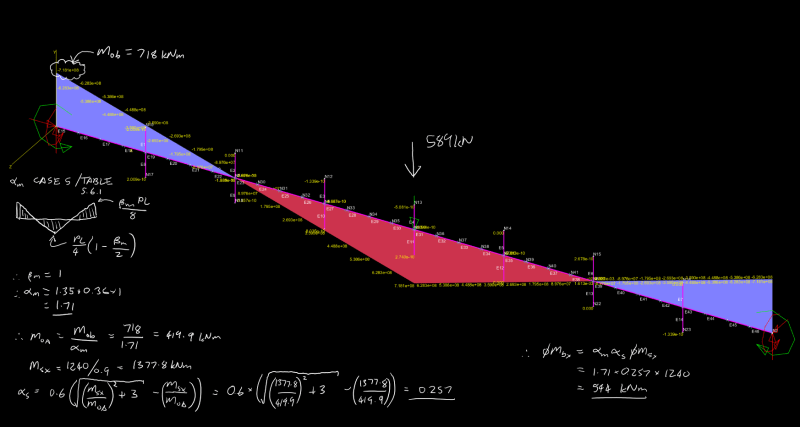
I think there might be a quick and easy first test we can apply. Taking the W27x84 and the same bi-linear shape of the moment diagram from the test case, I reduced the maximum bending moment to 1240 kNm which is the design section capacity phi.Ms. I then increased the sub-segment length until the AS4100 LTB capacity phi.Mb = phi.Ms. The sub-segment length was 5.065m (ie from end of beam to the inflection point) giving overall beam length of 20.26m before LTB governs according to AS4100.
If I may be so presumptuous, I believe KootK will have an opinion on whether this is realistic or not. If that opinion is that it is not, he may never 'drop his bone' and accept AS4100. That doesn't need to end the discussion but people may at least continue knowing that.
KootK said:
If the AS4100 provisions are so simple, derive them and post the derivation here.
I don't think this is a fair challenge. AS4100 is simple to apply. If you put aside the 'flange that moves further' and just take the compression flange as the critical flange, the challenge is deciding on whether you've got F, P or L restraints. With a small moving of the goal posts from 'simple to apply' to 'written simplistically', AS4100 is over-simple in this regard as it gives no numerical guidance - you just make a judgment, guided by some published examples of common connection details (or refer to other sources which set out stiffness requirements).
Deriving the AS4100 requirements with regard to this specific situation from first principles would be anything but simple. I suspect that many of the provisions were derived from basic cases like non-continuous beams, uniform moment etc and simply applied generally. I like to think the gurus considered the range of possible application and made a conscious (and correct) decision that AS4100 is close enough for government work but perhaps not and we just get lucky. Eg I found recently when discussing the Kt factor with Agent666 that it is known that the alpha,m factor (=Cb) can be quite unconservative for monosymmetric beams.

![[dazed] [dazed] [dazed]](/data/assets/smilies/dazed.gif)