Object X rams a wire. Does the wire break?

[kand16]

Hi,

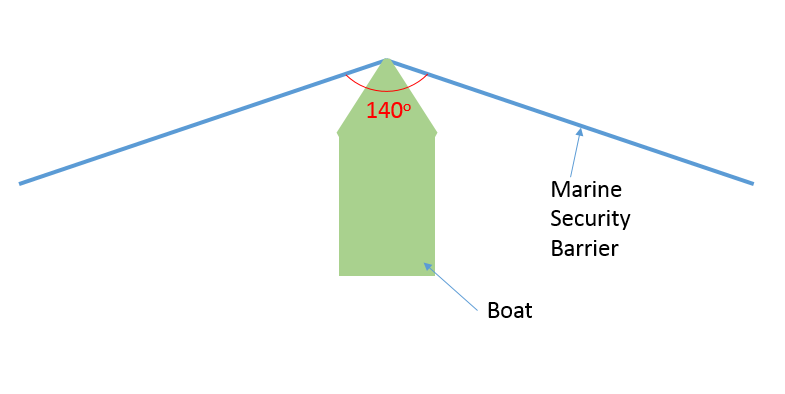
I'm trying to figure out how to use an object's defined kinetic energy to determine if its collision with a wire will break it, assuming the wire is weaker along its length than at its mounted ends. The real scenario is a motor boat with a KE of 40,000 Kg-Meter (shouldn't the doc's specs have this in kg-m²/s²?) is ramming a marine security barrier, and I need to figure out if the components in the marine barrier system will not fail. See image below of the security barrier system for concept.

To simplify my scenario I'm assuming my 19mm weldless end links are the weakest components in the system. They are made of AISI 1035 carbon steel (link for a materials property sheet I found:

http://www.azom.com/article.aspx?ArticleID=6540).

I'm also assuming the boat to be a "blob" that sticks to and combines with my system at impact, so that it doesn't skip and just graze the system. The barrier is not a taught line and I'm assuming there's enough slack for there to be a 140 degree angle in the system before it becomes "taught" by the boat (see image to clarify).

My initial path was to find the strain energy required to break my end links, but I'm uncertain how to do this as I can't find the AISI 1035 carbon steel's modulus of toughness and I don't know how to apply the referenced material properties into my strain energy in terms of the normal strain energy equation U_i = ∫^V(σ²/(2E))dV.

Another path I was thinking of, which seems improper to me due to the principles in the mechanics of materials, is finding the boat's impact force and seeing if this force is great enough to exceed my end link's UTS. Here, I'm uncertain of the slow down distance and not feeling comfortable to assume this figure.

Am I on the right path and can you help me? Should I be attacking this problem from a different angle?

Thank you for any help. I took my undergrad with classes in materials and mechanical engineering. It's become quite rusty.

 

[3DDave]

The cable is a spring element and the floats will tend to transfer energy to the water as they shift from their original position to the point contact position.

 

[itsmoked]

The floats will greatly slow the boat before terminal tension is reached.
The greater the angle the less the tension in the cable and end-points.

I wonder if there's a military manual (army core of engineering) on standard calcs for exactly this. They have to do pontoon bridges and harbors etc.

Keith Cress
kcress -

http://www.flaminsystems.com

 

[GregLocock]

It would be easy to model, difficult to calculate. Closed form solutions that feature drag proportional to v^2 are surprisingly hard to come by.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[BUGGAR]

Research log booms for dams. They are typically designed to restrain drifting logs. I worked on the Greenlake Dam and I don't remember who designed the log booms but they were designed much simpler - however they were considered an expendable "last ditch" element and they were isolated from the drinking public.

 

[LittleInch]

If you transfer the energy to Joules and then work on a perfect transfer of boat kinetc energy to line stretch of the wire rope ( you need to know or guess the area of the rope) that will end up giving you a force on the rope and hence your connectors.

You could assume some sort of loss of energy to e.g. the floats so only say 75% of the boat energy gets transferred, but start with 100% as the worst case - the impact might lift the floats out of the water so they might not lose much energy there.

what's "modulus of toughness?" The key number you need is Youngs modulus which is 200 x 10^9Pa

you seem to be neglecting the force of any propeller??

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[rb1957]

won't the boat ride over the cable ?

In which case, I'd expect the prop would probably do more damage.

If the boat doesn't ride over the cable, I'd expect it'd behave more like an icebreaker ... bow up over the cable, boat down onto cable, maybe breaking cable ...

another day in paradise, or is paradise one day closer ?

 

[kand16]

Thank you all for the help. I'll be responding to LittleInch as I'm looking for a way how to calculate this without needing simulation software.

Hi Little Inch,

Yes that sounds like the right way I want to calculate this problem. I have the energy in Joules, and I'm taking the worst case that all energy is transferred into the wire.

The "modulus of toughness" is the area under a material's stress-strain curve until failure. I figured if I know this then I can figure out if the wire rope can absorb the boat's energy without failing. With this in mind, does this mean the longer my wire rope is the less likely it will fail?

Using Youngs modulus, how do I use this to determine failure? Youngs modulus is characterized as a force over an area, whereas the boat is impacting it with an energy of 40,000 J. I know that if I had an impact distance I could use this to determine the impact force, but I don't have this value. Is there a way for me to figure out the modulus of toughness using the material properties page I found? Or should I be calculating this a different way?

Yes, I'm neglecting any force from a propeller. The specs call for "The barrier will absorb direct impact Kinetic Energy of 40,000 Kg-Meter."

 

[rb1957]

badly written spec ... how sharp a bow on the "object" ? I suspect that the cable may absorb a blunt body, but break with a pointed one. (btw, it wasn't the propeller force I was mentioning, but the cutting action of the propeller.)

if we had a dollar for every impact problem that's been posed "if I had an impact distance I could use this to determine the impact force, but I don't have this value" we'd be rich !

if we had a dollar for every problem that wanted a quick and ready (and accurate) answer without testing or simulation, we'd be rich !

In my mind this is a very complicated problem ... how does the cable drag across the water (in response to the impact) ? (this would probably be an efficient way of distributing the impact energy). Is impact energy the right measure ? (does mass trade-off with the square of speed ?) If the impact is close to an end I suspect that the cable will be more vulnerable than if impacted mid-span. How long is the cable ?

etc

another day in paradise, or is paradise one day closer ?

 

[Nescius]

Another consideration:

I can envision a scenario where the cable would break even if it were not anchored at the ends. Even if it's just floating there, the force required to accelerate that long line of barrier floats could be very large. Thus, even if the ends were anchored, they may not be subject to any force. Instead of working like a giant reverse slingshot, the cable would break somewhere between the impact and the anchor, at the point where there were simply too many floats along for the ride.

 

[Compositepro]

The energy that the cable is capable of absorbing is its ultimate tensile strength times its strain to failure. Then consider the other details.

By the way, chain link fence makes a great crash barrier for this type of application, particularly when you want to minimize damage to the vehicle.

 

[SwinnyGG]

You have a hard number that tells you the amount of energy you need this system to absorb.

You have a cable of known (I'm assuming, as you appear to be designing the system) characteristics.

Treat the cable as a spring. Potential energy contained inside a spring is a very simple formula:

U = (kx^2)/2

Where k = spring constant x = spring displacement, and U = stored energy.

Your stored energy and spring constant are known, solve for x.

Since you know your spring constant, once you know your displacement you will know the forces going into the end fittings of the cable as well es the total strain of the cable.

You can then use the strain value and force value to determine if the cable survives.

There is a little bit of slightly trick geometry to do, but once you know the cable stretch you will also know the stopping distance of the boat. Since you are disregarding drag on the system due to water, this estimate will be very conservative.

 

[racookpe1978]

Big boat with near-vertical but deep bow (ferry, ocean-going ship) will trap the wire and floats, then expend energy slowing down the ship by stretching the bable, then begin pulling out the anchors, and (if the anchors don't break loose from the shore pilings) then breaking through the line.

Small boat (typical lake or pleasure boat) will ramp up over the cable and floats, then probably "trap" the cable between boat and outboard motor propeller. Which will then suddenly stop the boat and snag the boat as it slams it down to the water while pulling out the outboard and flipping up the motor to a traveling position. Cable will not likely break at all if greater than a 1/4 inch wire rope.

Large boat/pushboat/river floating industrial craft - These have a modestly shallow draft and a long flat bow with a lot of overhang. The push boat/"towboat" will go over the wire and floats very easily and not be stopped at all until the push boat's far deeper draft and propeller/shaft/rudder snag the wire many minutes later. Wire will break and eventually will wrap around the propeller shaft and cause minor problems. Barges and towboat will not stop for any realistic wire diameter and anchor design.

 

[LittleInch]

Leaving aside the practical issue of whether the boat would actually catch the wire or not, the current issue is force.

My theory, which might be an error, is this:

Your wire starts as straight wire but not under tension.

As the boat hits the wire it extends the wire, straining the wire elastically.

The strain (delta L) can be calculated or just initially assume say 1%.
The stress that will induce in the wire is 2 x 10^Pa (N/m2). You know the square area of your wire (I don't), but this stress will give you a force f.

Energy is then that f (divided by 2) x deltaL to take account of the increase in force linearly as the wire stretches

This gives you the potential energy in the wire which if you play around with the strain ( so long as it remains in the elastic zone) will then equal the boat energy in the most conservative case.

Also gives you your force on the end connectors.

All very simplistic and subject to many more issues, but should get you a handle on the force required and whether the wire will take the load or not. If you get beyond 5% strain then your wire is probably not in the elastic zone any more and I would limit it to 2% to start with unless you know the yield stress of your wire....

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[Artisi]

Ask the navy, they see this same senario evertime a plane lands on an aircraft carrier.

It is a capital mistake to theorise before one has data. Insensibly one begins to twist facts to suit theories, instead of theories to suit facts. (Sherlock Holmes - A Scandal in Bohemia.)

 

[LittleInch]

Artisi,

Not really - the wire is connected to a drum which is braked and unwinds, hence why the air craft doesn't suddenly shoot backwards off the carrier when it stops...


More like a farmer if a bull decides to run into a wire fence....

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[Artisi]

LittleInch; correct but they are probably the best source of info. - whatever info. is available.
It would be necessary for the navy to understand the likely failure mode for a fault in arrest system.

It is a capital mistake to theorise before one has data. Insensibly one begins to twist facts to suit theories, instead of theories to suit facts. (Sherlock Holmes - A Scandal in Bohemia.)

 

[LittleInch]

I would imagine that is a broken plane....

This is just a nice theoretical physics problem.

the chance of it actually doing what it is supposed to do is nearly zero. It would either break the wire or the boat or sink the boat or slip off the front end and decapitate the crew or ....

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[GregLocock]

"Ask the navy, they see this same scenario everytime a plane lands on an aircraft carrier." And I've seen the MBD sim that has been used, as opposed to trial and error, which is fun but expensive and/or painful.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[kand16]

LittleInch is right that I'm isolating the practicalities of this problem and turning it into just a physics problem. Thank you jgKRI and LittleInch for the help on the relation between springs and materials.

Focusing on this from an energy perspective, I now see I can use the conservation of energy to solve this.

I found the equation for calculating the modulus of toughness: u_t=(1/3)ε_fracture(σ_y+2σ_u), which is in J/V

My identified material properties of the AISI 1035 Carbon Steel to use for the weldless end links are:
E = 200 GPa
σ_y = 370 MPa
σ_u = 585 MPa
ε_y = 0.00185
ε_fracture = 0.3

Therefore, my modulus of toughness is 154x10⁶J/m³

Now finding my forged end links cross-sectional area to use for the area of the wire rope, I have an area of 5.678x10^-4m² from a 19mm end link size.

I have assumed a length of 2m, with the boat hitting dead center resulting in a 1m L.

With these values I have

U_t = u_tV = (154x10⁶ J/m³)(5.678x10^-4m³ x 1m) = 87.3 KJ

which is the ultimate energy needed to break my link.

If I'm assuming the boat to hit the chain in the diagram in my opening post, then each side is 1/2 of 40,000 J, or 20,000 J.

Using geometry I have 20,000 / sin(20 degrees) = 58,476 J of energy acting against my chain. This is well below the requirement to break my chain!

Thank you all for the help. I hope this will help others who have a similar scenario.