Foundation stiffness is EI where E is Young's modulus and I is the moment of inertia. You will also need properties of the soil. Deflection is dependent on both of those. A beam on an elastic foundation is a fairly advanced type of calculation. I suggest you assume the beam to have infinite stiffness or, in other words, that it acts as a rigid body. Or in still other words, the soil pressure will be assumed to be linear.
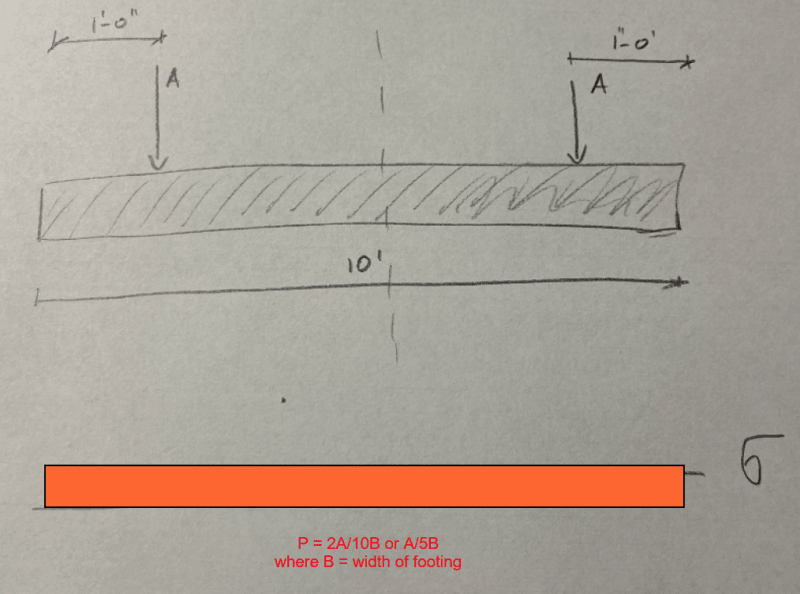
If the load is not symmetrical, find the c.g. of load. If it lies within the kern of the foundation, use the formula given by Celt83 above.
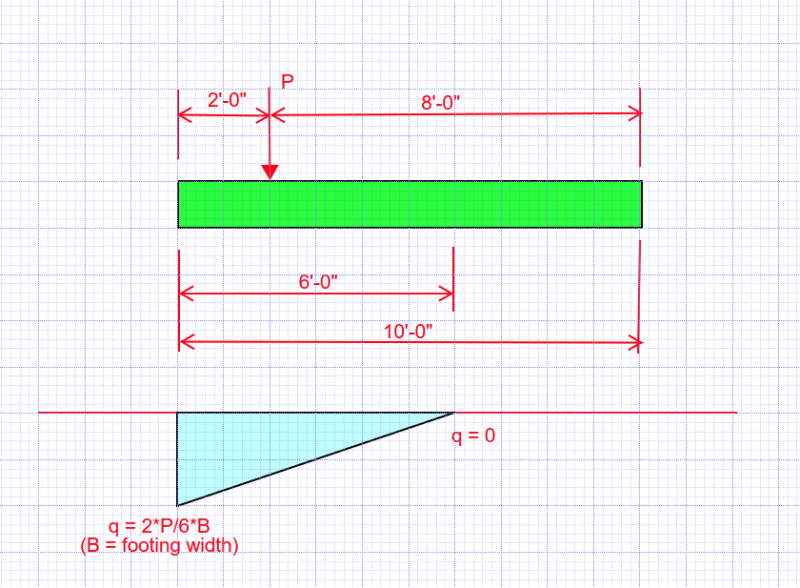
If the c.g. of load 'P' is outside the kern of the foundation, there will be a point where the pressure equals zero. That will occur at a distance 'D' from the end nearest the c.g. The maximum pressure will be at the end and will have magnitude of twice the average pressure, or 2*P/B*D.
Effective length D = 3*C where C is the distance between the end of foundation and the c.g. of load.
For your foundation, the kern of the section is the middle third of the 10' length. If the eccentricity is less than 10/6 = 1.667', it is within the kern, so:
Pressure 'q' = P/A +- P*e/S where A is area of contact and S is section modulus.
If e > 1.667, then the effective length of footing is 3*C;
so qmax = 2*P/3*C and qmin = 0.
Beyond the effective length, the footing rises off the ground and pressure is zero.