Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations JAE on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
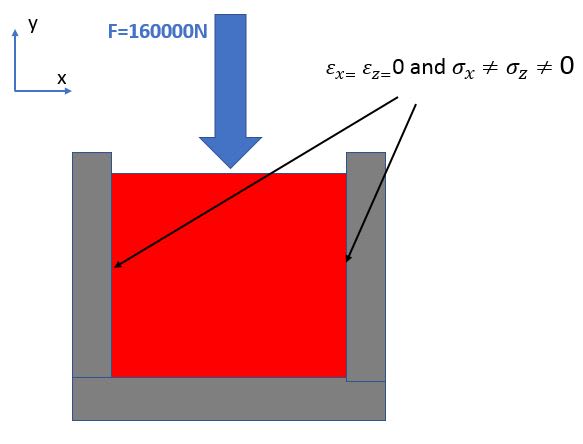
how can I calculate the stress in X- and Y-direction
- Thread starter aliex
- Start date
- Status
- Not open for further replies.
Erik Panos Kostson
Structural
Not sure exactly what you mean, but from what I can see:
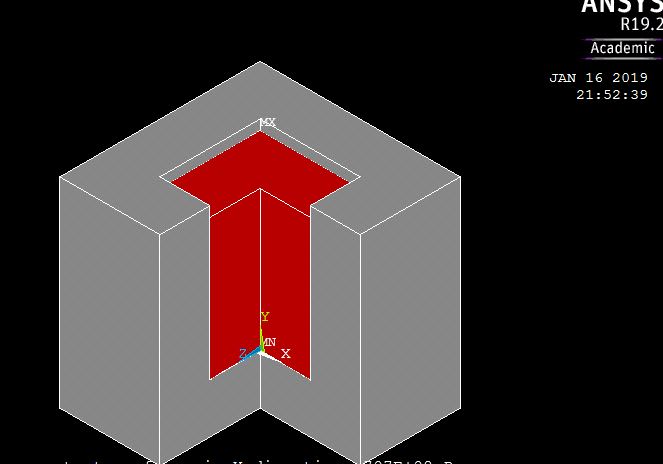
In your first picture, there is a contact between the red and grey block (that is the appropriate boundary condition).
Once you load the red block on top, with the contacts (e.g., frictional) assigned (and some support/fixed, for the gray part so it does not move freely), you will be able to see stresses along different directions (say SXX or SYY,...).
Hope this helps.
In your first picture, there is a contact between the red and grey block (that is the appropriate boundary condition).
Once you load the red block on top, with the contacts (e.g., frictional) assigned (and some support/fixed, for the gray part so it does not move freely), you will be able to see stresses along different directions (say SXX or SYY,...).
Hope this helps.
- Thread starter
- #3
Erik Panos Kostson
Structural
Plane stress (thus stress in z is zero):
σy= F/A
σx= ν*σy
Plane strain (thus strain in z is zero):
σy= F/A
σx= ν/(1-ν)*σy
σz= ν*(σy+σx)
σy= F/A
σx= ν*σy
Plane strain (thus strain in z is zero):
σy= F/A
σx= ν/(1-ν)*σy
σz= ν*(σy+σx)
- Thread starter
- #5
Erik Panos Kostson
Structural
Well look at the plane strain solution σz is not zero. Finally if you rearranged these you get that σx= σz.
According to the elasticity constitutive relation, stress_vector = C_matrix * strain_vector, where the vector has a size of 6, and C_matrix is the stiffness with the size of 6x6.
If your material is isotropic and linear elastic, both strain_x and strain_y are zero. To determine the stress_x and stress_y, you only need to know C13, C23, and strain_Z.
If your material is isotropic and linear elastic, both strain_x and strain_y are zero. To determine the stress_x and stress_y, you only need to know C13, C23, and strain_Z.
- Status
- Not open for further replies.
Similar threads
- Question
- Replies
- 0
- Views
- 2K
- Locked
- Question
- Replies
- 0
- Views
- 1K
- Locked
- Question
- Replies
- 2
- Views
- 1K
- Locked
- Question
- Replies
- 1
- Views
- 3K
- Replies
- 9
- Views
- 1K