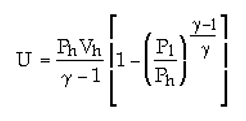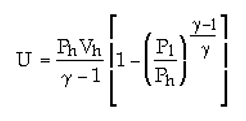It looks like all three equations are the same but in different form. The equations are for obtaining the work (energy) for the very slow quasi static expansion of a gas from a high to low pressure (like in a piston cylinder arrangement). This is the maximum possible energy that can be extracted from the gas.
The first equation indicates that for air for an isothermal process the polytropic exponent "n" factor is 1.0 and for an isentropic process the same factor is 1.4. So when the gas is expanding, if heat is added in enough quanity while it is expanding the gas will remain at constant temperature during the expansion and the exponent will be 1.0 for a constant temperature expansion. If there is no heat input to the gas during expansion then the temperture will drop since the energy of the gas is going into the work to push against the piston (or surroundings) and no heat is coming in to keep the gas at constant temperature. If there is no heat input and there is no irreversible losses then the process is isentropic where the exponent "n" is 1.4 and the temperature drops during the expansion in accordance with the isentropic expansion temperature relationship equations. Note for an isentropic process the exponent is the same as the ratio of specfic heats, so for air Cp/Cv = 0.24/0.17 = 1.4 the isentropic expansion exponent. A polytropic process is one that is somewhere between an isothermal and isentropic process and the exponent "n" is called the polytropic exponent "n" rather than the isentropic exponent "k".
In a typical expansion the process is somewhere between isothermal and isentropic which puts the polytropic exponent somewhere between 1.0 and 1.4. For instance if you are expanding a gas in a piston-cylinder arrangement as you expand the gas it is picking up heat from the walls of the cylinder and depending on how hot the cylinder is will determine how much the expansion goes from isentropic to isothermal and therefore how much the expansion goes from isentropic 1.4 to isothermal 1.0 factor. In your case of a gas exploding in a vessel I think the process will be closer to isentropic as not much heat can be picked up from surroundings that fast.
The second equation looks like the same equation but in different terms and assuming an isothermal process with n=1.0. It even states that and isothermal process was considered in the write up.
The third equation is the same as the first with "gamma" replacing "n" and making other substitutions to just change the form a little.