BAretired
BAretired
No need to apologise, now I'll take the blame for continuing the discussion.

It is nuanced because the VQ/I is an inherently correct formula from theoretical fundamentals. Though how it understood and applied is more nuanced than people can realise. For example, from a calculative perspective there is nothing in the calculation telling WHERE the shear needs to be transferred and there is nothing even to require that the elements be contiguous (connected or each other).
Furthermore there is NOTHING in that formula that involves "picking a point".
So this notion of only calculating shear flow at a point and especially only calculating Q in one direction (eg upward or downwards) is fundamentally flawed no matter what a textbook says. (Though typically the boundary between two areas becomes the point or plane where one is choosing to consider the shear flow.)
EG;
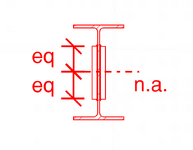
View attachment 14869
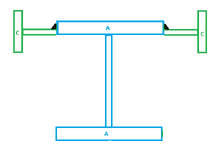
This section on the left still has a calculable V, Q & I. You can calculate the shear flow required between A & B but all that tells you is that VQ/I shear must be flowing between A and B, even though there is no obvious way it can nor an obvious way for V to be identical and thus one might rightly question that it is a indeed a single section. So we can fix that.
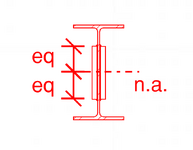
View attachment 14871
Now we are looking at something a little more familiar. We can calculate V,Q,I and work at the shear demand at any point. we want. That break between section A and B can be anywhere we choose. Also we can work out Q on whichever area we choose. The normal way of calculating the above would be to calculate the Q of section B. But you can just as easily calculate the Q of section A and get the same answer. If we choose to calculate the Q for section A we get a value of ZERO for the web of A and the value of Q of section A flange is equal to the B flange. So that all checks out, something would be amiss if the VQ/I gave different results if you choose the opposite section.
View attachment 14872
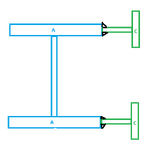
Likewise we can go nuts calculating the shear flow in this double-I section however you want. But if you choose to calculate Q of (A&B) or (A' & B') then you will get Q=0. You can call it a compound section as much as you want. You can weld those flanges together if you choose. However as long as you can ensure that V is equal then the VQ/I=0 and there is no shear flow. The original example is no different. There is no shear flow between the plates and the beam because Q =0
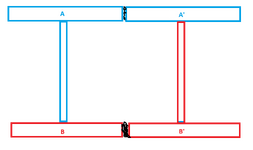
View attachment 14873
I hope this example above will convince you against the perverse notion of picking a point and only calculating Q above or below it. If I was going to size the welds for section C I'd consider ALL of the area of C to calculate Q, not just the bit 'above' my weld.
Oh, and there is one more method of analysis that I found really useful graphically and match up to calculated results within a 5%.
I modelled two beams
-200mm deep, 100mm wide flange, 10mm thick web and flange, point loaded with 100kN, 2m long
The top beam exactly matches hand calcs as the section is drawn perfectly. The lower one is slightly out because it is actually made of a grillage of members (20x10mm).
View attachment 14874
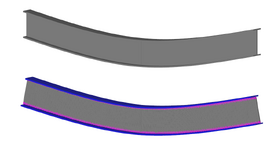
Because this is a grillage you can readily see the shear flow in discrete elements. A grillage of 1D elements is a poor man's 2D or 3D FEA. But it is often more interpretable and user friendly than FEA.
View attachment 14875
You can measure and visually see the shear flow and also the shear lag around the supports. My measured value is 5.63kN of shear per 20mm, the hand calculated value is 5.91kN. So 5% out, but it isn't a perfect model but it is good to play around with and observe the shear flow. I also found it quite satisfying to see the shear flow at the top add up in 20mm segments to equal the total axial load in the flanges at centre. Again something you should expect but satisfying to see it incrementally and visually.
I also modelled the example of the I beam with plates. The result is as expected, no shear flow as there is no stress/strain differential between the plates and the web. If people are interested I can post more. But I think this post has been long enough.