Mechanical design/Math rotating bars

There are entire books on mechanical linkages.
This is simple geometry.
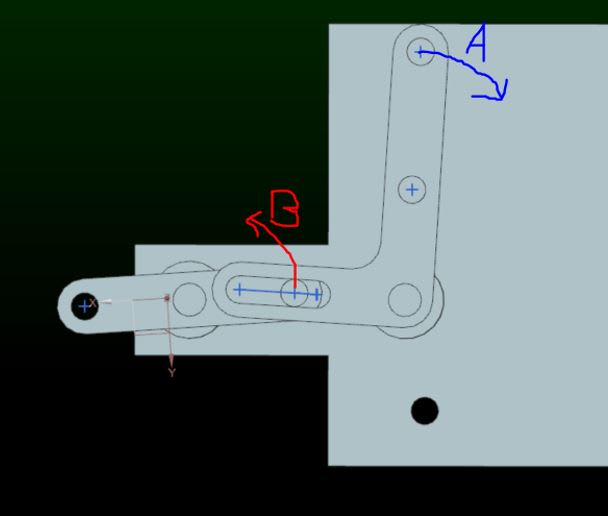
You are actually interested in the movement of the hole in the end of "B" aren't you?

= = = = = = = = = = = = = = = = = = = =
P.E. Metallurgy, consulting work welcomed

Hint: It's not a linear relationship for more than infinitesimal travel.

EdStainless yes I am interested in the movement in the hole in B

Did you have a class in trigonometry?

3DDave Yes

This is not unlike some of the mechanisms that I worked with when I was a machine designer. The primary purpose was to convert a constant input motion into a variable output motion. In fact, we patented a mechanism which we called the 'variator' that used this principle, that is a cam follower, attached to the crank arm on one rotating shaft, retained in a slot on a second crank arm attached to a parallel rotating shaft. The distance between the centerlines of the two parallel shafts determined the profile of the curve which represented the rotational speed of the output shaft relative to the rotational speed of the input shaft. Note that the length of the slot in the second arm was long enough that the shafts were able to rotate a full 360 degrees . This was used when we needed a portion of a mechanism to start slow, speed-up and then slow down again before the end of a cycle. The input shaft was driven through a single rotation clutch, which when activated only allowed the shaft to make one rotation. The clutch was cycled for each desired output cycle (I wish I had a picture).

John R. Baker, P.E. (ret)
Irvine, CA
Siemens PLM:

The secret of life is not finding someone to live with
It's finding someone you can't live without

You should know the distance between the pivots and the distance from the one pivot to the pin marked B. You know the angle of the slot relative to the baseline between the two pivots.

So, recalling that C^2 = A^2 + B^2 - 2 ABcos(theta) and you know C, you know A, you know theta you can calculate "B", the distance from the first pivot to the place along the slot the pin is. Knowing all three lenghts you can calculate all three angles; in this case the remaining 2 of which you are interested in only one.