Please see the below script I have created to solve the problem. It doesn't work. Can some one help?
clear; close all; clc;
syms x1(t) x2(t) x3(t) x4(t);
r=[-0.05 0 0.03 0.05;
0.05 -0.05 0 0;
0 0.02 -0.02 0;
0 0.03 0.02 -0.05];
D=[0;1;4;0];
X=[x1;x2;x3;x4];
odes=diff(X)==r*X+D;
x1Sol(t)=simplify(x1Sol(t));
x2Sol(t)=simplify(x2Sol(t));
x3Sol(t)=simplify(x3Sol(t));
c=X(0)==[0;0;0;0];
[x1Sol(t), x2Sol(t), x3Sol(t), x4Sol(t)]=dsolve(odes,c)
Consider four ponds connected by streams. Initially, the ponds were pristine.
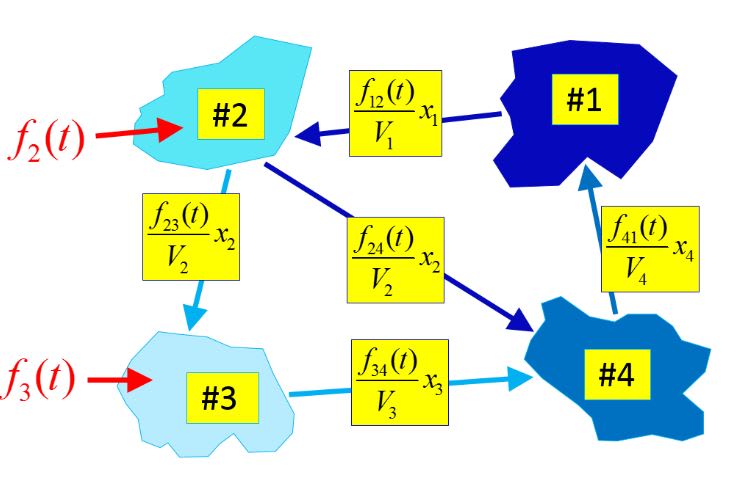
At time t=0, after environmental accident, the second and third ponds are getting polluted with the sources, releasing pollutant substance with the following rates: f2=1 kg/h and f3=4 kg/h. Pollution spreads via the connecting streams to the other ponds, as shown in the Figure.
For this task, formulate associated differential equations in terms of x1(t), x2(t), x3(t) and x4(t) - time functions, describing pollutant amounts in each lake. Solve problem numerically, using ode45 MATLAB procedure, and DETERMINE the amount of pollutant (in kg) in lake #2 towards the end of 48 hours of contamination. For a specific numerical example, take f12/V1=f41/V4=0.05; f23/V2=f34/V3=0.02; f24/V2=0.03 [all in 1/h].
Figure-2: Four ponds #1, #2, #3 and #4 of volumes V1, V2, V3, V4 [all in m^3], connected by streams with specific flow rates f12, f13, f23, f34, f41 [m^3/h].
Formulate system of the first order ordinary differential equations and solve it numerically, using ode45 procedure.
clear; close all; clc;
syms x1(t) x2(t) x3(t) x4(t);
r=[-0.05 0 0.03 0.05;
0.05 -0.05 0 0;
0 0.02 -0.02 0;
0 0.03 0.02 -0.05];
D=[0;1;4;0];
X=[x1;x2;x3;x4];
odes=diff(X)==r*X+D;
x1Sol(t)=simplify(x1Sol(t));
x2Sol(t)=simplify(x2Sol(t));
x3Sol(t)=simplify(x3Sol(t));
c=X(0)==[0;0;0;0];
[x1Sol(t), x2Sol(t), x3Sol(t), x4Sol(t)]=dsolve(odes,c)
Consider four ponds connected by streams. Initially, the ponds were pristine.
At time t=0, after environmental accident, the second and third ponds are getting polluted with the sources, releasing pollutant substance with the following rates: f2=1 kg/h and f3=4 kg/h. Pollution spreads via the connecting streams to the other ponds, as shown in the Figure.
For this task, formulate associated differential equations in terms of x1(t), x2(t), x3(t) and x4(t) - time functions, describing pollutant amounts in each lake. Solve problem numerically, using ode45 MATLAB procedure, and DETERMINE the amount of pollutant (in kg) in lake #2 towards the end of 48 hours of contamination. For a specific numerical example, take f12/V1=f41/V4=0.05; f23/V2=f34/V3=0.02; f24/V2=0.03 [all in 1/h].
Figure-2: Four ponds #1, #2, #3 and #4 of volumes V1, V2, V3, V4 [all in m^3], connected by streams with specific flow rates f12, f13, f23, f34, f41 [m^3/h].
Formulate system of the first order ordinary differential equations and solve it numerically, using ode45 procedure.

