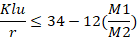Tek-Tips is the largest IT community on the Internet today!

Members share and learn making Tek-Tips Forums the best source of peer-reviewed technical information on the Internet!

Register Log in
  • Congratulations MintJulep on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!

Radius of Gyration of a Noncomposite steel and concrete section 2

Status
Not open for further replies.
Who_I_Am

Who_I_Am

Structural
Joined
Apr 28, 2022
Messages
5
Location
US
Hello, when calculating the radius of gyration (for moment magnifiers based on KL/r) for a non-composite steel and concrete circular section would you use the hollow steel section's 'r' value? If so, why? Can you provide me some code or AISC reference for this?

When researching this, Table 4-13 of the AISC 14th edition shows a composite section radius of gyration to be equal to the hollow HSS sections 'r'. Unfortunately there's no non-composite circular section 'r' value given in these tables. Any help is appreciated.
 
Sort by date Sort by votes
I guess no one is biting, but IIRC that is because the strength of the column should be designed as the sum of its components. If you have good reason to believe there is bond between the two (doubtful), you could use the modular ratio to calculate I and A values and you would get a modified r value.
 
Upvote 0 Downvote
Out of curiosity, I have to ask: why would you add both concrete and rebar into a steel CHS column and not account for composite action? There will be composite action (concrete is very strongly confined), and thus composite section stiffness (greater than only CHS stiffness) even if you decide not to calculate it.
 
Upvote 0 Downvote
In Australian/New Zealand composite code, r is defined as follows for the gross section for use in determining the compression capacity (believe its the same in Eurocodes).

Screenshot_20220429-230700_Dropbox_allomc.jpg




 
Upvote 0 Downvote
@canwesteng
there is no reliable bond between the two, ultimately, the non-composite stiffness of the two is an average of the concrete and steel, so we brainstormed it in the office a bit more and realized that the program we're using calculates the moment magnifier based on the entire cross section and if we consider it a concrete section, per AASHTO LRFD the max KL/r is 100, if we only consider steel, max is 120. However a non-comp section is a grey area when it comes to finding the "r". Do we use the "r" for steel hollow section or the entire section? Using only steel gives us a larger "r" and therefore a KL/r of 115, but using the entire section yields a KL/r of 143. However, based on the maximum demand at the bent location, where these columns are located, we only need the steel sections flexural (and shear) capacity to resist the governing factored loads. Therefore, we've found it reasonable to ignore the concrete in these calculations and consider steel only. Adding concrete shouldn't make it worse for the structure.


@centondollar

That is a good question, initially it was for two reasons, one being added stiffness for drivabliity (so the hollow section won't plug with soils when driving it 80 feet) and to produce a partially fixed connection from column to bent (only a small cage developed into the cap) but based on my response above, we only need the moment capacity of the steel section (only partially developed into the bent cap) to handle the maximum factored forces from Strength and Service load cases.

@Agent666
Thank you for the composite equation, however I was curious if I can just ignore the concrete in calculating the KL/r in this non-composite situation, as that would give me a value less than 120, which per AASHTO is acceptable to have for a column.
 
Upvote 0 Downvote
Are you using Chapter I of the spec? It goes into depth on determining direct bond interaction for composite action in filled members, force allocation procedures, etc.
 
Upvote 0 Downvote
@phamENG

I'm not considering composite action between the concrete and steel, it's a 16" steel section, 1" thick that's 80 ft long, there's no feasible construction method to weld shear bolts all along it to make it behave like a composite section.
 
Upvote 0 Downvote
Right. There's also no feasible construction method to weld shear bolts along the length of the inside of a 6" pipe column, but that doesn't stop the SCM from listing composite section properties. That's because, in Chapter I, there's a set of equations that you can use to evaluate the effective bond between the steel and concrete in contact with one another. It's nowhere near as good as headed studs on, say, an encased composite member, and the phi/omega factors give some hints as to the variability of the effect, but it's there and can be relied upon. There's some info in the commentary.

If you really don't want to...then it also says that the column shouldn't be any weaker than the steel section without concrete fill.
 
Upvote 0 Downvote
Yeah currently we really don't need the concrete for any additional capacity, the 16" hollow steel section can handle the axial and flexure demands it's subjected to so as a stand alone model it should be able to handle the loads there. Thank you for that input on the commentary, if we need to sharpen our pencils I'll look at the commentary and see what additional capacity I can take from that interaction, it must all be skin friction contribution right?
 
Upvote 0 Downvote
Who I Am said:
it must all be skin friction contribution right?
Click to expand...

Essentially. As centondollar mentioned above, the concrete is well confined and the friction between the two is sufficient to cause composite action.
 
Upvote 0 Downvote
Regarding composite behavior.

1) I'm pretty sure that, somewhere, AISC will let you do composite action for a wide flange beam with external concrete and no mechanical connection. So "bond" is certainly a real thing.

2) I'd certainly be hesitant to rely on bond for composite behavior in something that you intend to beat the heck out of during piling.

3) When it comes to resisting flexural demand, I've found interior concrete fill to be pretty ineffective. That, because:

a) Shrinkage within a long member pretty much guarantees that you have to assume the concrete to be cracked, even if the cracks are small and well distributed as one would hope.

b) Interior concrete, especially cracked interior concrete, doesn't operate at much of a flexural lever arm.

4) I'd be comfortable using the concrete for axial loads but:

a) You can probably do this without composite action anyhow.

b) Shrinkage and creep mean that your axial load will tend to migrate over to the steel anyhow.
 
Upvote 0 Downvote
KootK said:
2) I'd certainly be hesitant to rely on bond for composite behavior in something that you intend to beat the heck out of during piling.
Click to expand...

I've only done this once (maybe twice?), so I'm far from an expert, but we had bottom plates welded to the pile and drove it hollow. Then concrete was poured into the pile from a barge. Seemed to work out pretty well.
 
Upvote 0 Downvote
I've been noodling on the kL/r issue for a few days now. In the process, I've realized that my understanding of the nature of those checks has been pretty superficial. Yes, it's a check against "slenderness" but what exactly does that mean and how do you extend that to a non-conventional situation? Here's what I think kL/r means based on the derivation of the equations that we use:

1) You want a member not excessively prone to P-baby-delta moment amplification under axial load.

2) Since apparent flexural stiffness approaches zero as the axial load approaches the Euler buckling load, achieving #1 means controlling the ratio of the applied load to the Euler buckling load.

3) To simplify matters for #2, we do the kL/r check without involving the applied axial load. To manage that, we instead assume that the designer intends that the member will achieve some, reasonable ratio of it's squash load (As x Fy, Ag x f'c). Whether that ratio is 0.3, 0.5, or 0.7, I don't actually know.

4) In conclusion, [kL/r < WHATEVER] is a comparison between the Euler buckling load and the squash load of the member. I feel that the important takeaway from this is that the Euler load and the squash load are calibrated to be associated with:

a) The same cross section.

b) materials having the same stiffness.

c) Materials having the same max stress (Fy, f'c).

So, applying this to OP's practical question, here's what I come up with:

A) If OP's steel section is designed to deal with 100% of the moment and axial load, then kL/r < 120 is surely appropriate.

B) If it will be the concrete taking some or all of the axial load then kL/120 will still be appropriate so long as the total axial load does not exceed the squash load of the steel section. That, because in this situation, the steel section alone is still stiff enough against lateral movement that it is capable of stabilizing this amount of axial load whether it resides in the steel or the concrete.

C) If the concrete will take some of the load, and that load is greater than the squash load of the steel section, then kL/r < 120 is no longer appropriate. That, because in this situation, the steel section alone is not stiff enough against lateral movement that it is capable of stabilizing this amount of axial load.


 
Upvote 0 Downvote
Thank you KootK, this falls within the A) scenario, and it is drivable so no squash load (i like that term). I believe that this design is okay because you're judgement is similar to our understanding. Thank you all for your contributions.
 
Upvote 0 Downvote
I'm not familiar with the US code references, but moment magnification/amplification becomes less accurate as the second order effects increase. One measure of this is the magnitude of the amplification factor which takes account of the load as well as slenderness. Another measure is the raw slenderness which gives a measure of sensitivity of the results.
 
Upvote 0 Downvote
KootK said:
4) In conclusion, [kL/r < WHATEVER] is a comparison between the Euler buckling load and the squash load of the member.
Click to expand...

Not sure if already considered in the noodling, but column curves tend to lie slightly above:

N_squash/[1 + (N_squash/N_Euler)]

The weakest Australian steel compression curve (highest residual stress) follows this closely (within ~2% over the full range), while the other four are above it (and quite considerably in the inelastic region for the strongest couple of curves). But the trend is there. Similar for aluminium compression and steel bending, where that equation gets up to ~20% conservative at the worst match.

So, while concrete design doesn't use the column curve, this should give an estimate of where kL/r=100 lies in terms of capacity relative to squash load.
 
Upvote 0 Downvote
steveh49 said:
Not sure if already considered in the noodling
Click to expand...

No, I'd not considered that at all. Thanks for sharing your observations.

steveh49 said:
Another measure is the raw slenderness which gives a measure of sensitivity of the results.
Click to expand...

Can you elaborate on what you mean by "raw slenderness"? I get the impression that you see that as a load independent slenderness. Presently, I'm of a mind that there's really no such thing. Further to that, this has me wondering if there's a justifiable way to cheat these slenderness ratios. Consider:

1) kL/r = 120; the 120 is really [SQRT(E/Fy) x MARGIN]. This is a squash load comparison.

2) If I want to sharpen my pencil, could I sub in the real axial stress as [SQRT(E/Fa) x MARGIN]. This is a slenderness comparison based on the real load.

In this way I feel as though one could say that they have a kL/r > 120 but still satisfy the requirement if kL/r < SQRT(E/Fa) x MARGIN].

Congratulations on being the Eng-Tips Grand Wizard last week! For seven days and seven nights, your word is law.

 
Upvote 0 Downvote
I meant kL/r when I said raw slenderness. Moment magnification is mentioned as the reason for the question being raised and I came from the Australian perspective where the kL/r=120 limit in our code (compared with AASHTO's 100) is just a limit on the moment magnifier method. We can push past if we do a higher-tier analysis. So I suspect the same applies to the AASHTO code, but don't know for sure. That would rule out cheating based on structural behaviour as it's the simplified analysis method that is being limited.

In terms of where the limit sits between 100 & 120, I'd be happy with a sliding scale based on relative contribution of EcIc & EsIs to the total EI.

Correct me if wrong, but ACI 318 doesn't have the kL/r limit, just the limit on second order effects compared to linear effects? That seems to be similar to how you would want to 'cheat' AASHTO.
 
Upvote 0 Downvote
Regarding ACI limits, I found this article which might be helpful.

American Concrete Institute (ACI) [..] defines the criteria for the effect of slenderness ratio. The slenderness ratio can be neglected for compression members braced against sideways when

image020_cijjbo.png
 
Upvote 0 Downvote
Status
Not open for further replies.

Similar threads

Nayan67
  • Question Question
slab design of noncomposite girder
Replies
4
Views
2K
KootK
KootK
S
  • Locked
  • Question Question
Flush joist of rolled steel section. HE 220B and CLT
Replies
2
Views
1K
shpata
S
D
  • Locked
  • Question Question
Calculation of concrete foundation for steel fence
Replies
14
Views
6K
Damned
D
murphy89
  • Question Question
Bending Class of Reinforced Steel Beams
Replies
2
Views
7K
dik
dik
Ron247
  • Question Question
Lateral Pressure of Flowable Fill concrete against a basement wall
2 3
Replies
44
Views
7K
Tomfh
Tomfh

Part and Inventory Search

Sponsor

Back
Top