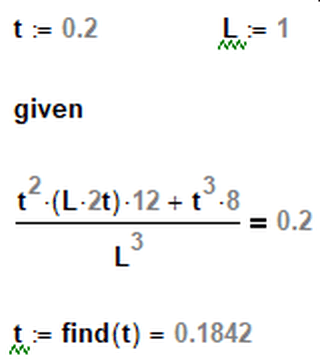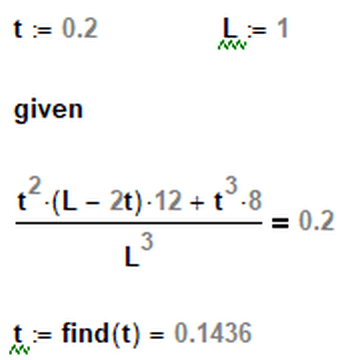I exploit the symmetry of fig.1 to simplify it to fig.2. This figure has a volume fraction of 0.2, and I need to find a relation between t and L. Have I done it right?
Volume of cube in the middle: (L-2*t)^3
And 4 rectangular plates around the cube in the middle: t*(L-2*t)^2
Volume of fig 2 is then: L^3 – ((L-2*t)^3 + t*(L-2*t)^2)
So volume fraction is that volume divided by the unit cell cube volume, giving:
(L^3 – ((L-2*t)^3 + t*(L-2*t)^2))/L^3 = 0.2
Which gives the relation:
t = 0.0428787 L

Volume of cube in the middle: (L-2*t)^3
And 4 rectangular plates around the cube in the middle: t*(L-2*t)^2
Volume of fig 2 is then: L^3 – ((L-2*t)^3 + t*(L-2*t)^2)
So volume fraction is that volume divided by the unit cell cube volume, giving:
(L^3 – ((L-2*t)^3 + t*(L-2*t)^2))/L^3 = 0.2
Which gives the relation:
t = 0.0428787 L