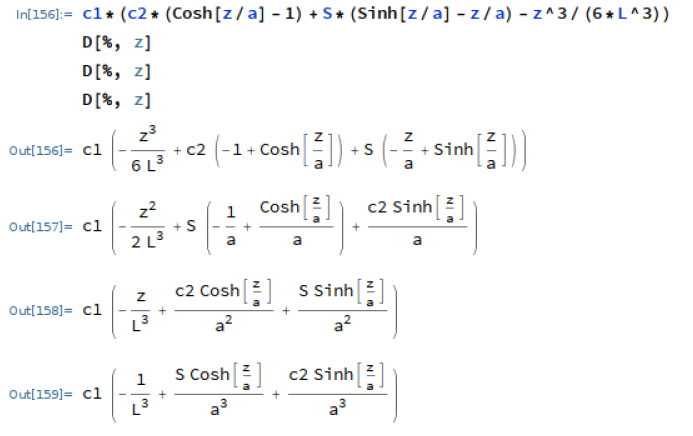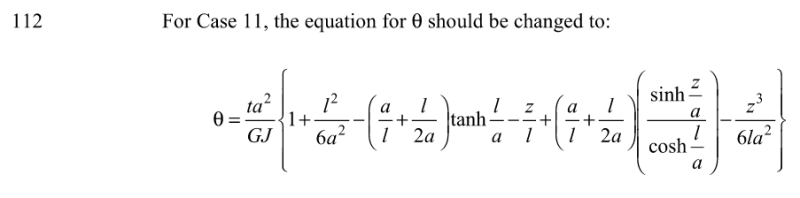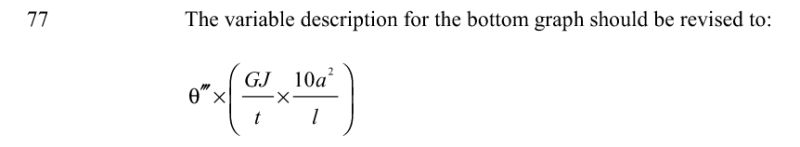Torsional functions - Derivatives 5

Something like the attached if you can marry up the different cases?

Alternatively take derivatives like noted in upper right on 1st page.

They are likely from AISC Design Guide #9 on Torsion.

Dik

See this thread:Link

And look for the starred post by structSU10

My Personal Open Source Structural Applications:

Open Source Structural GitHub Group:

Thank you very much to both for this publication.

Assuming theta is a function of Z, a lot of the complicated terms are just constants relative to z, so I think the derivatives would work out easier than it might look.

I have been through these charts based on the documents in this post.
The discrepancies I wanted to bring up include the following (see attached):
- Case 5 (θ''): My results are similar for the larger values of L/a but there is a discrepancy at smaller values. For L/a = 1, tabulated max is -0.14 and I get about half of this.
- Case 8 (θ'): Similar to above, my results tend to increasing discrepancy as L/a approaches zero.
- Case 8 (θ'''): My results are out by a factor of 10 compared to the literature. Is it possible the latter is missing a factor of 10?
- Case 11 (θ''): I think there is an error in the formula for the second derivative.

The literature from AISC did have at least one mistake, in Case 3 (θ), the original values have been overwritten.

Can someone please verify my results for Cases 5 and 8.

Does anyone have any experience with this?

LR11 - I'm actually gearing up to write a paper on torsion, and the design guide and associated technical note will play a big part in that. When I get into it I'll try to review the points you've brought up and see what I can figure out.

Sure no worries, we can compare data in due course.

Definitely case 11 is incorrect, as you've proposed it should be a negative sign (output from Mathematica):-

Note you can simplify further to be in a similar form to the AISC equations by factoring the 'a' terms and recognising that sech=1/cosh.

I did a small writeup here

I wonder for some of the other cases if AISC kind of screwed things up in case 5 in plotting due to the weird scale in the attachment you provided, where by the first division is 0-0.15 and the other divisions being the same vertical height but only 0.05 between divisions? Seems like a potential error to me?

don't know what occured at the end of that post with the attachments. There are no attachments. Can't seem to edit it out.

Case 8 derivatives also seems correct (the same as AISC versions), no factor of 10 in there sorry.

Case 5 derivatives also seem correct (the same as AISC versions)

Thanks for spending so much time on it, and confirming the error in case 11.
With respect to cases 5 and 8, and the differences between my plots and the curves supplied in Appendix B: I re-plotted and have the same outcome as in post "23 Feb 20 12:48" ... it wasn't the derivatives I was questioning in these instances.
- The subtle difference in Case 5 (θ'') and Case 8 (θ'): Who knows?
- The factor of difference in Case 8 (θ''') : The plot axis shows θ''' x (GJ/t x a^2/L) ... my suggestion was that it should be θ''' x (10GJ/t x a^2/L).

The observation that there was an inconsistent plot scale in Case 5 (θ'') & the AISC amendment for Case 3 (θ) may suggest that some plots have errors in them.

Hi LR11

It doesn't take much time at all to run them through Mathematica.

Yeah you'd tend to think their plots have some errors in the case of the derivatives being validated as being correct. The other option is that the original angle formula being started from may be wrong!

I did just note they have recently updated the errata for DG9.
This includes a revision to the original angle formula for case 11 to:-


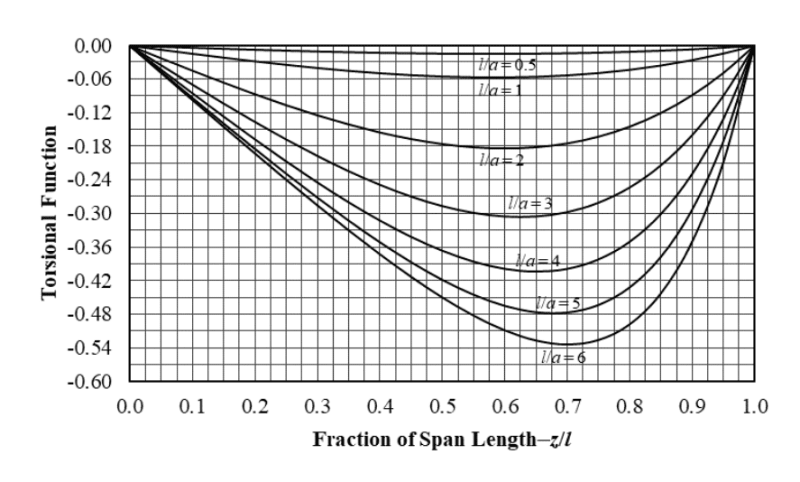
They also have updated case 5 graph for the 2nd derivative which is one of the cases you are comparing, which compares much better with your graph:-


For case 8 page 77 bottom graph the graph is actually now noted as being for:-

So you are right it is out by a factor of 10.

Check out the latest errata as there are a few other errors noted for other cases you haven't mentioned.

So on the balance of probabilities I'd imagine you have it correct, and they are probably wrong. I'd feedback any of the errors you think are there to AISC. Reality is most people have probably just plugged and chugged and not actually checked the formulas as you have!

Updated derivatives for case 11, note subtle changes in 1st derivative and sign change in 2nd and 3rd derivatives compared to previous result:-

Thank you again for advising of the errata list.
I will go through the others amendments as well.
Cheers.