My main question has to do with how you mathematically treat an uplift load when doing overturning calcs. I have seen 2 different ways but they do not yield the same answer. Currently I am reviewing an older structure for new loads but the old design did not calc them the same as I do. Just thought I would see how the Eng-Tips world does it. I have always used all stabilizing forces divided by all destabilizing forces as the formula for FOS. This is definitely the conservative method. I have seen many times where they are treated as net forces and then the FOS is calculated.
The attached drawing shows a fdtn with a horizontal and vertical applied forces. The upper set of calcs is net forces while the lower set is (all stabilizing/all destabilizing). The 2 methods do not matter if the FOS is 1. It only matters when the FOS is not 1.
Just curious how this is treated by others. The more loads and the higher the FOS is, the more the footing weight amount differs.
Also would like a good layman's explanation of how the 300# vertical load can cause overturning about the left and right sides simultaneously. Other than statics says it will. It seems that if the fdnt is not truly attached to the ground on one of the sides, it would only create uplift but not overturning. In that situation, the net force method seems appropriate to some degree.
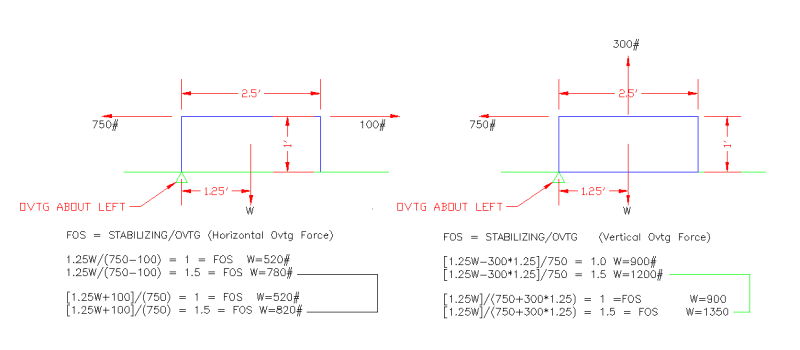
The attached drawing shows a fdtn with a horizontal and vertical applied forces. The upper set of calcs is net forces while the lower set is (all stabilizing/all destabilizing). The 2 methods do not matter if the FOS is 1. It only matters when the FOS is not 1.
Just curious how this is treated by others. The more loads and the higher the FOS is, the more the footing weight amount differs.
Also would like a good layman's explanation of how the 300# vertical load can cause overturning about the left and right sides simultaneously. Other than statics says it will. It seems that if the fdnt is not truly attached to the ground on one of the sides, it would only create uplift but not overturning. In that situation, the net force method seems appropriate to some degree.