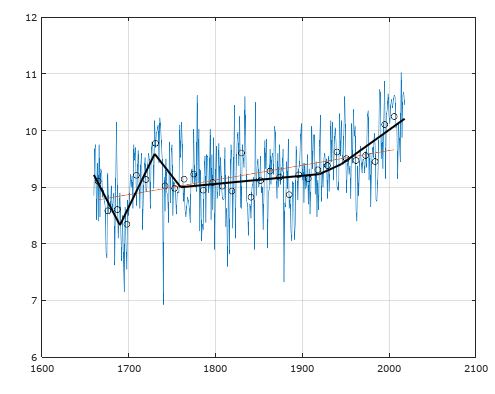
function p = fitPiecewiseLinearFunction(x, y, x0)
%
% Fit a piecewise continuous function f(x) to the pairs of data points (x,y)
% such that the sum of squares of error is minimal.
%
% x0 - values of x that define ends of segments of function f(x)
%
% p - end points of the segments p = f(x0)
%
% See also: [URL unfurl="true"]http://golovchenko.org/docs/ContinuousPiecewiseLinearFit.pdf[/URL]
%
% 4-May-2004 Nikolai Golovchenko.
%
numberOfParameters = length(x0);
% separate data in segments
j = {};
for i = 1 : numberOfParameters - 1
j{i} = find(x > x0(i) & x <= x0(i + 1));
if isempty(j{i})
error('Insufficient amount of data points');
end
end
% compute the matrices corresponding to the
% system of equations
A = zeros(numberOfParameters, numberOfParameters);
B = zeros(numberOfParameters, 1);
for i = 1:numberOfParameters
if i ~= 1
% first sum
A(i, i-1) = A(i, i-1) - ...
sum((x(j{i-1}) - x0(i-1)) .* (x(j{i-1}) - x0(i))) / (x0(i) - x0(i-1)) .^ 2;
A(i, i) = A(i, i) + ...
sum((x(j{i-1}) - x0(i-1)) .^ 2) / (x0(i) - x0(i-1)) .^ 2;
B(i) = B(i) + ...
(sum(x(j{i-1}) .* y(j{i-1})) - x0(i-1) * sum(y(j{i-1}))) / (x0(i) - x0(i-1));
end
if i ~= numberOfParameters
% second sum
A(i, i) = A(i, i) + ...
sum((x(j{i}) - x0(i+1)) .^ 2) / (x0(i+1) - x0(i)) .^ 2;
A(i, i+1) = A(i, i+1) - ...
sum((x(j{i}) - x0(i)) .* (x(j{i}) - x0(i+1))) / (x0(i+1) - x0(i)) .^ 2;
B(i) = B(i) + ...
(-sum(x(j{i}) .* y(j{i})) + x0(i+1) * sum(y(j{i}))) / (x0(i+1) - x0(i));
end
end
% find the parameters
p = A^-1 * B;

![[banghead] [banghead] [banghead]](/data/assets/smilies/banghead.gif)
![[bowleft] [bowleft] [bowleft]](/data/assets/smilies/bowleft.gif) Wow, cute names, too...
Wow, cute names, too...