Eng-Tips is the largest engineering community on the Internet

Intelligent Work Forums for Engineering Professionals

Register Log in

Breaking a 2d cloud of data points into straight line segments

Status
Not open for further replies.
GregLocock

GregLocock

Automotive
Apr 10, 2001
23,120
1
36
Orbiting a small yellow star
I recently found a couple of ways of doing this. They are not automatic, and i suspect they need some judgement in their use.

The first is from Matlab
and the second is the very neat SLM curve fitting toolbox
When i get matlab back then I'll be using these.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376
 
Here's a rather splendid piece of code that does most of what I need. That is, for a given set of knots in x0 it generates contiguous best fit straight lines for the x and y vectors. The result, p, is the y at the defined x0. What it doesn't do is measure the error, or attempt to move the knots to reduce the overall error. That of course, is what i need.

Code: 
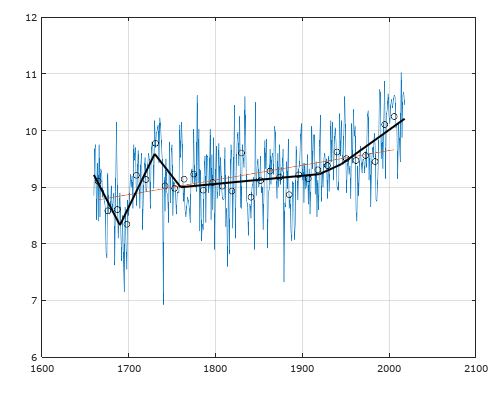
function p = fitPiecewiseLinearFunction(x, y, x0)
%
% Fit a piecewise continuous function f(x) to the pairs of data points (x,y)
% such that the sum of squares of error is minimal.
%
% x0 - values of x that define ends of segments of function f(x)
%
% p - end points of the segments p = f(x0)
%  
% See also: [URL unfurl="true"]http://golovchenko.org/docs/ContinuousPiecewiseLinearFit.pdf[/URL]
%
% 4-May-2004 Nikolai Golovchenko.
%


numberOfParameters = length(x0);

% separate data in segments
j = {};
for i = 1 : numberOfParameters - 1
   j{i} = find(x > x0(i) & x <= x0(i + 1));
   
   if isempty(j{i})
      error('Insufficient amount of data points');
   end
   
end

% compute the matrices corresponding to the
% system of equations
A = zeros(numberOfParameters, numberOfParameters);
B = zeros(numberOfParameters, 1);

for i = 1:numberOfParameters
   if i ~= 1
      % first sum
      A(i, i-1) = A(i, i-1) - ...
         sum((x(j{i-1}) - x0(i-1)) .* (x(j{i-1}) - x0(i))) / (x0(i) - x0(i-1)) .^ 2;
      A(i, i) = A(i, i) + ...
         sum((x(j{i-1}) - x0(i-1)) .^ 2) / (x0(i) - x0(i-1)) .^ 2;
      
      B(i) = B(i) + ...
         (sum(x(j{i-1}) .* y(j{i-1})) - x0(i-1) * sum(y(j{i-1}))) / (x0(i) - x0(i-1));
   end
   if i ~= numberOfParameters
      % second sum
      A(i, i) = A(i, i) + ...
         sum((x(j{i}) - x0(i+1)) .^ 2) / (x0(i+1) - x0(i)) .^ 2;
      A(i, i+1) = A(i, i+1) - ...
         sum((x(j{i}) - x0(i)) .* (x(j{i}) - x0(i+1))) / (x0(i+1) - x0(i)) .^ 2;
      
      B(i) = B(i) + ...
         (-sum(x(j{i}) .* y(j{i})) + x0(i+1) * sum(y(j{i}))) / (x0(i+1) - x0(i));
   end
end


% find the parameters
p = A^-1 * B;

The black line is an eyeballed set of knots for the blue data. The circles are 11 year moving averages and the orange line is just a linear regression.

golov_f18vms.jpg



I looked at two built in functions. 'splinefit' tries to equalise the segment lengths. 'polyfit' doesn't guarantee that the lines are contiguous at the knots.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376
 
Try this. You can try several numbers of specified joints, and pick the 'Best' number based on rms error.

x=1:100;
y(1:25) = 0+rand(25,1);
y(26:50) = 1+rand(25,1);
y(51:75) = 2+rand(25,1);
y(76:100)= -1+rand(25,1);
figure
plot(x,y,'r.')
hold on

sp3=spap2(3,2,x,y) % 3 joints, 1st order( use a 2 for 1st order )
fnplt(sp3,'m')
 
 https://files.engineering.com/getfile.aspx?folder=20b527e5-015a-4ea2-89e6-7889d52fc5ea&file=Smoking_3_joints.JPG
Settle on the number of knots the science seems to suggest, apply lsqcurvefit (Matlab) to the knot locations and turn the crank. I picked 11. Once you get the first solution, bootstrap it by perturbing the lsqcurvefit solution and send it back into the fire a few more times. I do this technique with Pacejka tire model fits and it works very well.
 
 https://files.engineering.com/getfile.aspx?folder=5231943f-49b1-4fde-893e-07c348f2b619&file=Knots_Landing.JPG
Status
Not open for further replies.

Similar threads

AitorKo
  • Question
Work in Matlab with a reduced model in Abaqus
Replies
0
Views
24
AitorKo
AitorKo
Arash Nasiri
  • Locked
  • Question
importing a prepared mesh (FEM) into Matlab
Replies
1
Views
14
Mohanlal0488
Mohanlal0488
udlondy
  • Locked
  • Question
How do I model cloud security in Matlab/Simulink
Replies
1
Views
4
IRstuff
IRstuff
TEIF-RO
  • Locked
  • Question
How to do a reccurent substitution in a symbolic matrix in matlab withor the ''FOR'' loop?
Replies
4
Views
17
GregLocock
GregLocock
TEIF-RO
  • Locked
  • Question
obtaining a NORMALISED POWER SPECTRUM DENSITY
Replies
2
Views
7
IRstuff
IRstuff
Back
Top