Hi
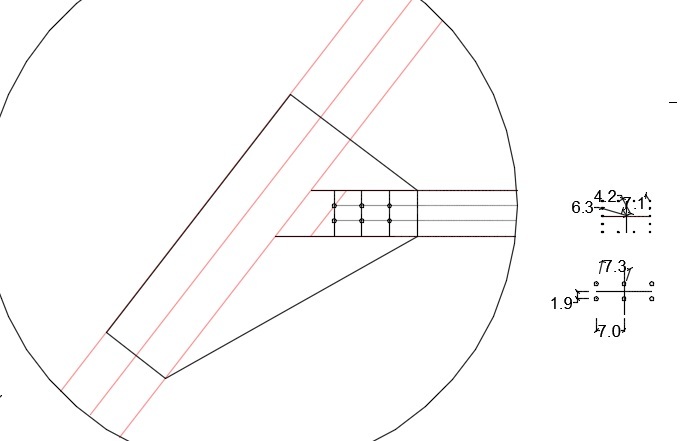
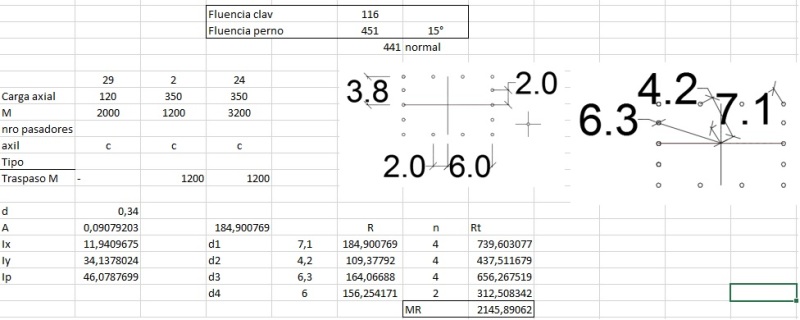
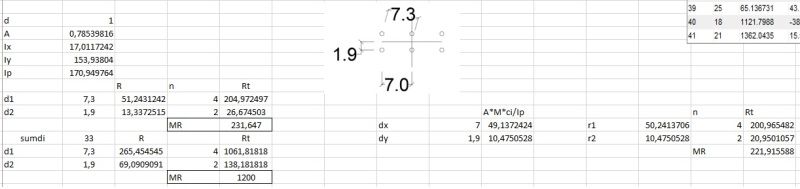
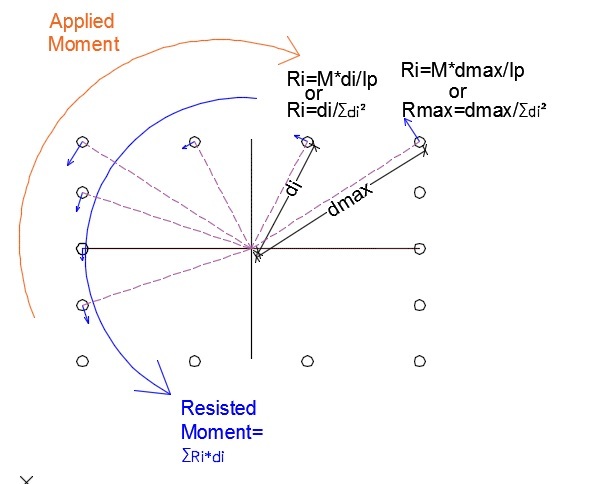
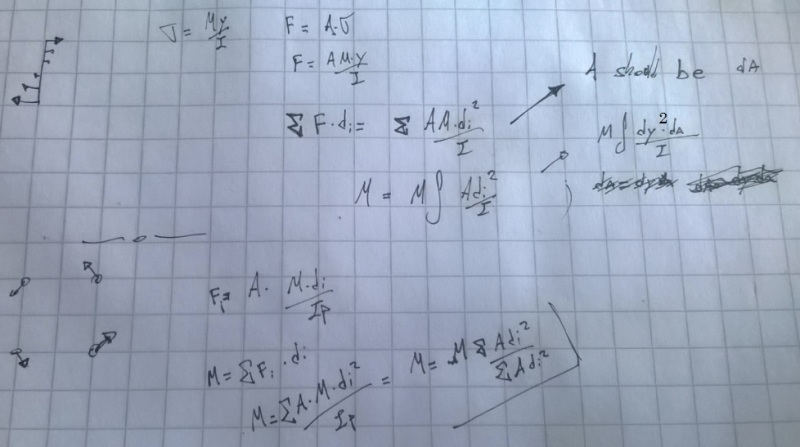
I been working with the center of rotation to estimate the reaction on bolts groups with the expression Ri=M*di/Ip. Where M:Moment, di: distance from center to bolt and Ip: Polar Inertia.
Ip=Ix+Iy
Ix=summation(A*dyi^2)
Iy=summation(A*dxi^2); (Parallel axes Inertia, but ignoring bolt inertia for being small)
My doubt begins while trying to match the acting moment with the resisted moment by the group by using the following
Resisted Moment= summation(Ri*di)
My reactions are pretty smalls and the resisted moment is also small. But makes no sense with the applied moment.
I also tried to decompose the forces by axis thinking that i had a confusion when measuring the distance directly from the center of rotation to each bolt center.
There is another approach which takes reactions as follows:
Ri=M*di/summation(di^2)
This method obviously match the applied with the Resisted moment, but i think that this method is just an extension of the Resisted Moment expression stated before.
Am I getting it wrong? is it Ok to have relative small reaction because the Ip? Any guide?
Thanks
I been working with the center of rotation to estimate the reaction on bolts groups with the expression Ri=M*di/Ip. Where M:Moment, di: distance from center to bolt and Ip: Polar Inertia.
Ip=Ix+Iy
Ix=summation(A*dyi^2)
Iy=summation(A*dxi^2); (Parallel axes Inertia, but ignoring bolt inertia for being small)
My doubt begins while trying to match the acting moment with the resisted moment by the group by using the following
Resisted Moment= summation(Ri*di)
My reactions are pretty smalls and the resisted moment is also small. But makes no sense with the applied moment.
I also tried to decompose the forces by axis thinking that i had a confusion when measuring the distance directly from the center of rotation to each bolt center.
There is another approach which takes reactions as follows:
Ri=M*di/summation(di^2)
This method obviously match the applied with the Resisted moment, but i think that this method is just an extension of the Resisted Moment expression stated before.
Am I getting it wrong? is it Ok to have relative small reaction because the Ip? Any guide?
Thanks