Simple question on adverse pressure gradients

Hob63 · May 24, 2016

Hi all,

I have a simple quesiton on the pressure distribution over an aerofoil but I can't seem to conceptually visualise it.

I am starting to convince myself of the flow over a circle such as the image below:

The stagnation point is a region of obvious high pressure (Cp = 1.0) and zero velocity, as the flow moves upwards this is a movement from high -> low pressure (dp/dx < 0) and so is favourable, this translates to an increase in the fluid velocity. At the top of the circle the maximum velocity/lowest pressure is achieved. From the rear of the circle there is also a wake region/seperation region resulting in low pressure.

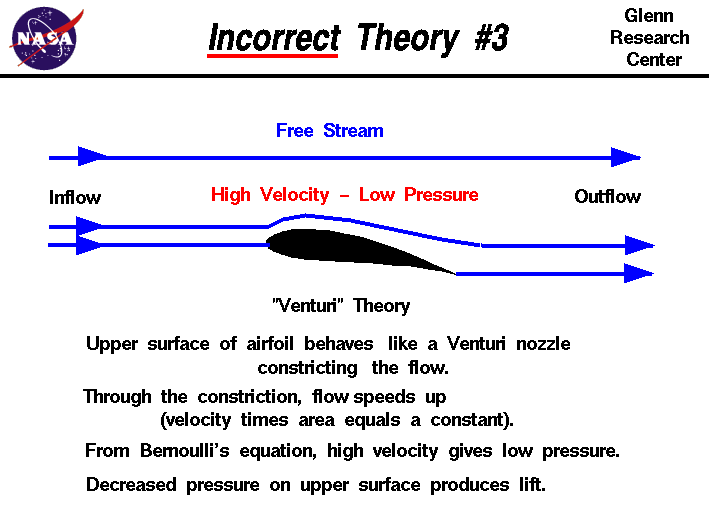
My question is why does the boundary layer seperate on the right but not the left, i.e why does a downward curve translate to an adverse pressure gradient, from NASA's website:

https://www.grc.nasa.gov/

http://www/k-12/airplane/wrong3.html

you cannot think of it as a simple venturi for the bulk flow with the freestream acting as a theoretical wall (although this would make it easier to understand).

Thanks for any info,

Hob

IRstuff · May 24, 2016

This site is not intended for student postings.

However, your premise about left and right being symmetrical is incorrect. You have a higher than nominal pressure on the left where the air is being compressed, so flow separation is impossible, but a lower than nominal pressure on the right, where the air is expanding. Separation is a fancy word for when all the air cannot follow the curve of the surface as it's expanding. There is a Wikipedia article:

https://en.wikipedia.org/wiki/Flow_separation

TTFN
I can do absolutely anything. I'm an expert!
faq731-376 forum1529

Hob63 · May 24, 2016

Many thanks for the reply,

For the flow regieme pictured I believe the flow is incompressible, I guess the confusing part is the low pressure on the rear of the circle. Via Bernoulli this would translate to a high velocity, but in reality it is seperated flow:

Is it that Bernoulli cannot be applied in the wake region due to the rotation of the flow?

IRstuff · May 24, 2016

Low pressure, in itself, is not an indication of high velocity flow. But, it's not solely the velocity that's at issue; it's also the geometry of the backside of the foil. Replacing the cylinder with a classical airfoil would result in substantially less, or no, separation, for the identical air flow conditions. Run the same cylinder at a slow speed and the separation gets smaller and can disappear altogether.

You can think of it as a "stickiness" of the boundary layer that breaks down and results in flow separation

TTFN
I can do absolutely anything. I'm an expert!
faq731-376 forum1529

btrueblood · May 25, 2016

Look at your graph at the 90 degree position. Here the pressure is at a minimum, and begins to rise again (recover) to the freestream value. Thus, dp/dx transitions from <0 before 90 degrees, to a positive value (adverse to flow) past 90 degrees. This positive pressure gradient gives rise to stalling of the boundary layer and flow separation.

Hob63 · May 25, 2016

This is correct btrueblood, but what is the reason for the adverse pressure gradient in the first place? perhaps a better image for my quesiton is this:

Why is point (4) adverse?, the flow is recirculating due to the pressure gradient, but why does downward curvature result in an adverse gradient in the first place?

The only theory on the subject I have seen is based on potential flow, but this would give rise to inviscid lift surely?

btrueblood · May 25, 2016

Go back to Bernoulli or potential flow (inviscid). Downstream of the obstruction, in the absence of friction, what would the pressure do? It should be increasing right? Therefore, the gradient along the flow direction must change from negative to a positive or adverse value. Add friction back in, and yes, the gradients get smushed around due to the blockage and losses, but the mechanism is the same.

Hob63 · May 25, 2016

But then on the application to a wing (the image above can be assumed to be the upper surface) NASA gives:

from:

https://www.grc.nasa.gov/

http://www/k-12/airplane/wrong3.html

"The part of the theory about Bernoulli's equation and a difference in pressure existing across the airfoil is correct. In fact, this theory is very appealing because there are parts of the theory that are correct. In our discussions on pressure-area integration to determine the force on a body immersed in a fluid, we mentioned that if we knew the velocity, we could obtain the pressure and determine the force. The problem with the "Venturi" theory is that it attempts to provide us with the velocity based on an incorrect assumption (the constriction of the flow produces the velocity field). We can calculate a velocity based on this assumption, and use Bernoulli's equation to compute the pressure, and perform the pressure-area calculation and the answer we get does not agree with the lift that we measure for a given airfoil."

So I am still at a loss as to the pressure gradient if the venturi effect for an aerofoil is incorrect.

KENAT · May 25, 2016

Angle of ~~the dangle~~ Attack, bound vortices, circulation, kutta condition, lifting line theory...

We had a full term class on fluid dynamics at uni that culminated in 'why a wing produced lift' and some members of the class still didn't understand (although they probably got better grades on the exam than me).

Posting guidelines faq731-376
http://eng-tips.com/market.cfm?
(probably not aimed specifically at you)
What is Engineering anyway: faq1088-1484

btrueblood · May 25, 2016

The venturi effect of an airfoil is not incorrect, just incomplete. The physics behind the Bernoulli equation are still in play in real life, and give rise to the adverse gradient. Adding friction into the equation complicates things, and getting the right values for the pressure gradient vs. location is not going to be predicted by Bernoulli alone, but by Bernoulli plus more complicated mechanisms. Adding the friction back in is the black art of fluid mechanics, and like Kenat says, is not something simple.

IRstuff · May 25, 2016

You seem to keep wanting to miss the point. The pressure gradient exists, but that's not all that's generating lift. The NASA picture shows the erroneous assumption about the vector of the air flow from the top of the wing resulting in the two bottom arrows on the right.

TTFN
I can do absolutely anything. I'm an expert!
faq731-376 forum1529

rb1957 · May 25, 2016

is this a student post ?

another day in paradise, or is paradise one day closer ?

Hob63 · May 25, 2016

rb1957 - I don't know but my questions are.

IRstuff - Lift as far as I can see arises due to the stagnation point on the lower surface of the wing and the curvature of the wing downwards, from momentum conservation there must be a resulting net upwards force. This is about the most qualitative accepted explination I can find.

The classical argument is simply there is a pressure difference resulting in an upwards pressure force 'lift', we can relate this to Bernoulli and state the velocity on the upper surface must be faster than the velocity on the lower surface, this arises due to the geometry of the wing. I haven't yet seen the reason as to how the geometry generates this velocity difference. Most state Bernoulli and the effective change in area giving rise to the velocity (the freestream and the wing surface acting as a venturi).

For a while I have been trying to see why more aerodynamicists haven't run into this problem, about the closest is Doug McLean and his book (I found yesterday), he gives an explination to the problem in his Youtube video:

https://www.youtube.com/watch?v=QKCK4lJLQHU

(from 15:11 to 27:56).

For me it is the arising of an adverse pressure gradient from the point of maximum wing thickness.

KENAT · May 25, 2016

Geometry of the airfoil has limited impact on whether or not it produces lift.

A relatively thin flat plate at an angle to the air flow will generate lift and display most of the same basic characteristics as a tear drop airfoil shape. In fact most initial labs at uni used flat plates not airfoil sections.

Likewise, symmetrical airfoils also generate lift and even asymmetric ones will generate 'lift' if the airplane is flown upside down.

(There are secondary characteristics which are impacted, just not fundamentally if they'll generate lift.)

Posting guidelines faq731-376
http://eng-tips.com/market.cfm?
(probably not aimed specifically at you)
What is Engineering anyway: faq1088-1484

Tek-Tips is the largest IT community on the Internet today!

Members share and learn making Tek-Tips Forums the best source of peer-reviewed technical information on the Internet!

Simple question on adverse pressure gradients

Hob63

New member

IRstuff

Aerospace

Hob63

New member

IRstuff

Aerospace

btrueblood

Mechanical

Hob63

New member

btrueblood

Mechanical

Hob63

New member

KENAT

Mechanical

btrueblood

Mechanical

IRstuff

Aerospace

rb1957

Aerospace

Hob63

New member

KENAT

Mechanical

Similar threads

Part and Inventory Search

Sponsor