Hi everybody,
I am struggling to find an analytic solution for the stress concentration due to a 3-D ellipsoid.
This article from Sadowsky and Sternberg dating back to 1949 dealt with the problem, and I tried to reproduce the same trend with the aid of a symbolic computation tool.
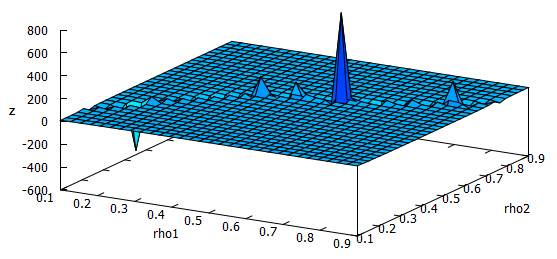
There must be something wrong somewhere since the resulting Kt as a function of the two shape ratios is the following:
Is there someone who can lend a helping hand?
Many thanks.
Best regards,
Mattia
I am struggling to find an analytic solution for the stress concentration due to a 3-D ellipsoid.
This article from Sadowsky and Sternberg dating back to 1949 dealt with the problem, and I tried to reproduce the same trend with the aid of a symbolic computation tool.
There must be something wrong somewhere since the resulting Kt as a function of the two shape ratios is the following:

Is there someone who can lend a helping hand?
Many thanks.
Best regards,
Mattia

![[ponder] [ponder] [ponder]](/data/assets/smilies/ponder.gif)