bluestar9k
Structural
When cross checking my work between Method of Joints and Sections I found the 2 methods produced different results for the same truss member.
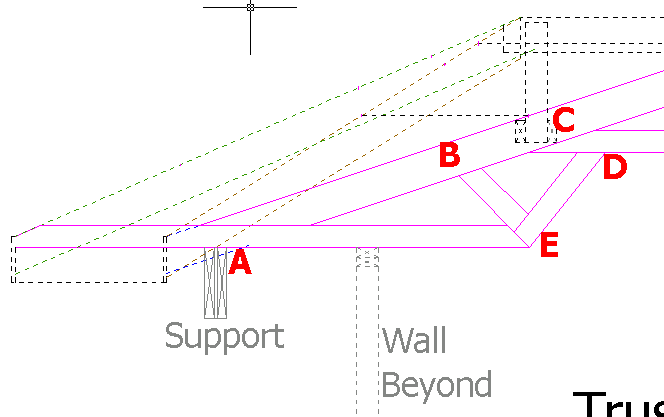
An image of the truss I am designing is attached.
I used an arbitrary reaction force of 529# at Nodes A & G.
Using Method of Joints the computed force in member BC is 1,673#.
Fbc = Reaction Force/sin(18.435) = 529#/sin(18.435) = 1,673#.
Using Method of Sections the computed force in Member BC is 1,038#
Take moment about node J and make a section cut between BC and JI.
Moment about J; Reaction Force*Distance = Fbc*Distance; 529#*37.47’ = Fbc*19.1’ … Thus Fbc = 1,038#.
19.1’ is the perpendicular projection from BC to J, determined mathematically and graphically.
1,673# does not equal 1,038# and I cannot determine why/where there is an error.
Any insight would be GREATLY appreciated.
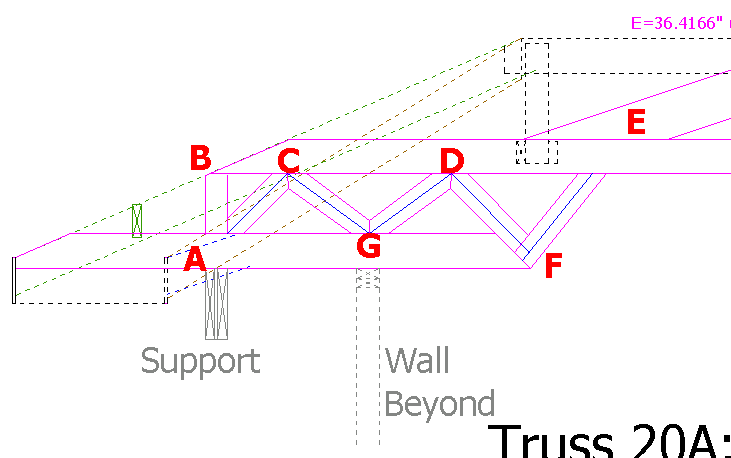
An image of the truss I am designing is attached.
I used an arbitrary reaction force of 529# at Nodes A & G.
Using Method of Joints the computed force in member BC is 1,673#.
Fbc = Reaction Force/sin(18.435) = 529#/sin(18.435) = 1,673#.
Using Method of Sections the computed force in Member BC is 1,038#
Take moment about node J and make a section cut between BC and JI.
Moment about J; Reaction Force*Distance = Fbc*Distance; 529#*37.47’ = Fbc*19.1’ … Thus Fbc = 1,038#.
19.1’ is the perpendicular projection from BC to J, determined mathematically and graphically.
1,673# does not equal 1,038# and I cannot determine why/where there is an error.
Any insight would be GREATLY appreciated.

![[idea] [idea] [idea]](/data/assets/smilies/idea.gif)
![[r2d2] [r2d2] [r2d2]](/data/assets/smilies/r2d2.gif)