Stepped Column with Unbraced Length 1

[sTRU_eNG89]

thread507-328375

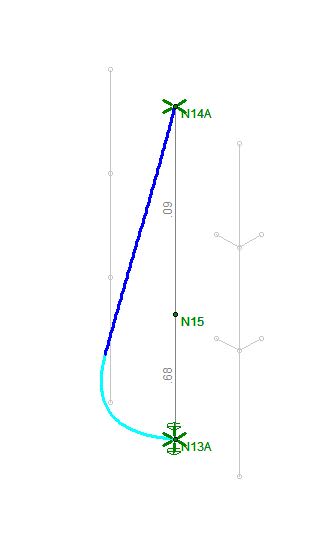
In the connected thread, the individual who posted the question is attempting to address a column that changes shape mid way up the building. Currently, In a project I am working on, I have a somewhat similar situation. We are creating a three story atrium space in the corner of a building, making the column in this corner un-braced for three stories, requiring reinforcement. The construction sequence requires the column be in a condition of reinforced for the upper two floors, while un-reinforced for the bottom third floor (15 ft floor to floor). Therefore, the column will be in a kind of 'reversed step column condition', where the bottom third of the three story span is significantly less stiff than the top two thirds.

I have done a decent bit of background research on step column design, but have come up dry for a formula or approach (other than Successive Approximations) for this kind of condition. While I believe the method of successive approximations will get me a result, it is very tedious. However, a response in the attached thread, by @WillisV's, presents a simple solution that I am curious about:

"Just analyze it with the direct analysis method. No issues with separate shapes. Model it with an initial sinewave bow equal to L/500, split it into several segments, reduce the stiffness, run a second order analysis - done."

However, I am a little confused how the separate shapes do not pose an issue in the second order analysis of this approach. Are the results of the second order analysis not dependent upon the stiffness and un-braced length of the column? If so, what is the stiffness of the column if the moment of inertia, "I", varies?

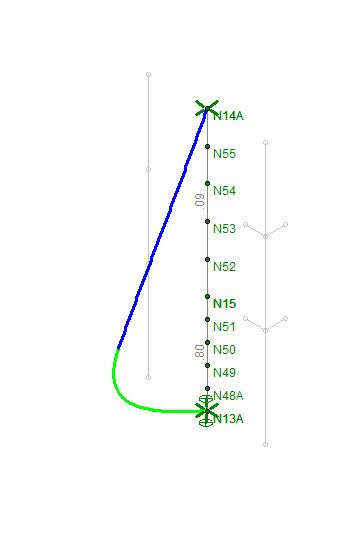
For example: If you input the two shapes (one 15ft long and one 30ft long) into RISA it will consider the unbranded lengths to be 15ft and 30ft, not the full 45ft. Providing inaccurate results. However, as an alternative, if you modeled a single, 45ft, column, how would you determine the needed "I" value for the second order analysis? Based on my research, it would appear that a weighted average of the "I" values is not adequate.

Is there something I am misunderstanding about the way in which a exact second order analysis is performed in computer programs?

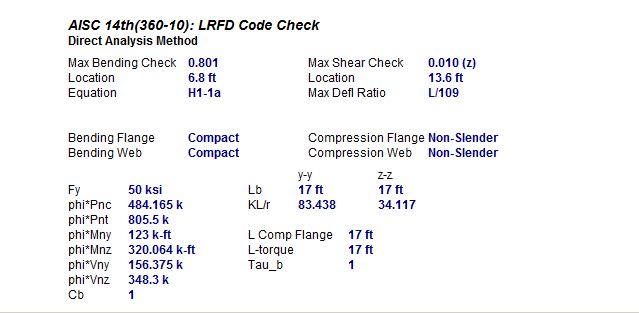
Maybe there is something I do not understand about the DAM? I know that the DAM requires the reduction of the stiffness of the member by 20% (.8EI) to account for residual stresses and system imperfections. However, I am not aware that this stiffness reduction accounts for a non-prismatic member. If that is the case, can anyone provide sources that show that?

Thank you in advance for any assistance and clarification provided here.

 

[ClearCalcs]

For example: If you input the two shapes (one 15ft long and one 30ft long) into RISA it will consider the unbranded lengths to be 15ft and 30ft, not the full 45ft. Providing inaccurate results. However, as an alternative, if you modeled a single, 45ft, column, how would you determine the needed "I" value for the second order analysis? Based on my research, it would appear that a weighted average of the "I" values is not adequate.

Are you sure this is the case? If you don't specifically put a brace there, I don't think any software will assume that it's braced at the intersection. If you want to make sure of this, I'd run the AISC second order benchmark cases (Section C2.J/p. 291 of AISC 360-16), and make sure it matches. Then split the benchmark member into two segments proportional to your 15 ft / 30 ft segments: the benchmark members are 28ft long so you'd end up with 9.33 and 18.67 ft long segments. Make sure values still match. If that's the case, then the model is essentially validated and I'd be confident with the analysis results when you switch your segment sizes.

-Laurent

http://www.clearcalcs.com

 

[sTRU_eNG89]

Laurent,

Thank you for your response. It would appear that you are correct and the program is only considering the segmented un-braced lengths for slenderness checks (KL/r), but is considering the entire column height (45ft) in the second order analysis. I believe this solves my problem, thank you. I will have to look into greater detail about the computational methods upon which the program performs the second order analysis.

Thank you

 

[dold]

Alex has a spreadsheet "STEPCOL.xls". I've never needed to use it personally, but I've attached it. I'd be curious to see how your results compare.

 

[sTRU_eNG89]

dold,

Thanks for responding to this thread. I downloaded the excel spreadsheet and it looks really well put together. From what I saw it calculates K values to be used for the columns in an approximate second order analysis (Appendix 8 in steel code) calculation. Is this correct?

Thank you

 

[JoshPlumSE]

Stru_Eng89 -

Let's first talk about what the DA Method will do for you and what WillisV was saying.

1) Notional Loads vs direct modeling of imperfections:
In your case, the reason why WillisV wanted you to model the initial shape as a sinewave curve. The reason for this is because this is the expected buckled shape. But, with an initial imperfection of only L/500.... Which represents initial out-of-straightness or out-of-plumbness of the column.

2) Stiffness reductions:
The purpose of this in the DA method is to take the "elastic buckling" that the analysis produces and get it to approximate the more realistic "In-elastic buckling" that your steel column is likely to experience.

3) P-Delta Analysis / 2nd Order analysis / Geometric non-linearity:
When you do a P-Delta analysis, the analysis results should do a good job of representing any ELASTIC buckling that occurs in the model. If your column is loaded above it's buckling limit, then the analysis will diverge. At loads approaching the buckling limit, you will get a lot of moment amplification directly in your analysis results.

Granted, for this elastic analysis to truly capture the buckling of this structure you need the initial imperfections from item #1 and the stiffness reductions from item #2 to approximate the INelastic buckling with your elastic analysis.​

Next, let's talk about the difference between modeling a member that's 30ft long vs two that are 15 ft long. There is NO DIFFERENCE in the analysis results of these cases if you are doing it correctly. The code checks may be different, but the moments, axial force, and deflections should be the same.

Finally, lets talk about the "code check" that program gives you. This is where using two 15 ft members may give a different capacity or demand / capacity ratio than using a single 30 ft member. However, if you manually entered in the same unbraced length for the various members, then they should still give identical results.

What I'm getting at is that the code check will be based on whatever "unbraced length" you enter for the member. In your case, this is still pretty tricky.

 

[sTRU_eNG89]

JoshPlumSE,

Thank you for the detailed explanation. You are correct, the issue I am truly running into here, is the code checks. The model is returning a code check for the bottom 15ft and the top 30ft, but not returning a check for the whole 45ft column.

Any ideas regarding a solution?

Thank you

 

[JoshPlumSE]

Considering you're relying so much on the P-Little Delta analysis (as part of the DA Method) to give you the buckling of this member, I would first use a few more nodes along the length of the column. Let's just say a node every 5 ft or so. At that level of meshing, you should really do a good job of capturing the P-Little delta effect.

What does the program say in the detail report about why it cannot give you a code check on the member? My guess is that you haven't entered an unbraced length, or have entered entered a value like the full 45 ft (which is conservative).

If you can get a better KL value from that spreadsheet Alex put together, then I'd enter that as the unbraced length and leave the K value as 1.0.

Note: I'm mostly guessing (based on the deflected shape that I'm seeing), but I'd say that the KL value should be something like 35 ft for the lower portion of the column. It certainly has to be less than 45 ft. The 35 ft number ends up being about 0.8 times the full height. Intuitively that seems about right. I feel like a value of 1.0 * the full height would be significantly too conservative, but a value of 0.5 * the height seems unconservative.

 

[Lomarandil]

Another source of an equivalent buckling length can be pulled from a Jan 1969 paper in AISC Engineering Journal by Dalal.

----
just call me Lo.

 

[robyengIT]

if it can help

 

[robyengIT]

and this too

and another thread

https://www.eng-tips.com/viewthread.cfm?qid=462330

 

[sTRU_eNG89]

JoshPlummSE,

Thank you for this assistance. I have added additional nodes along the length of the column in the model. This caused the utilization ratio of the lower section of the column to go up fairly significantly, but not above 1.00 (see photo). Please also see a snapshot of RISA's calculated KL values (for reference, the bottom portion is programmed as a W14x61 and the top portion an HSS18x18x3/4. You are correct that I did not enter an un-braced length in the column information. This is in an effort to allow RISA to calculate an effective un-braced length. However, based on what you mentioned, it appears that I may need to calculate my own KL value an input it manually.

This brings up one question I think is lingering for me that I don't seem to see a direct answer for the in the literature I have seen: is there a way to produce an effective length for the entire 'stepped' column? In doing so, allowing me to produce a utilization ratio for the entire column and forego the concerns that dividing the column into two pieces in the program is potentially causing an issue for the programs calculation of the critical buckling load and utilization values. The literature seems to consistently point to the use of an upper and lower KL value, which will inherently lead to a critical buckling load for the upper and lower segments respectively.