Acing
Mechanical
- Mar 4, 2016
- 8
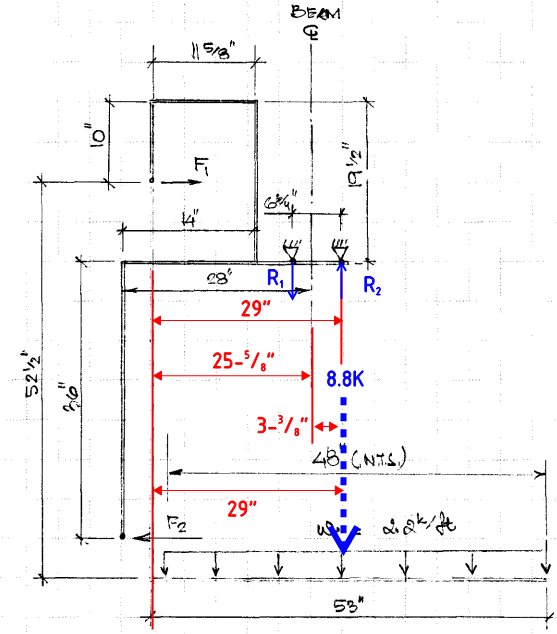
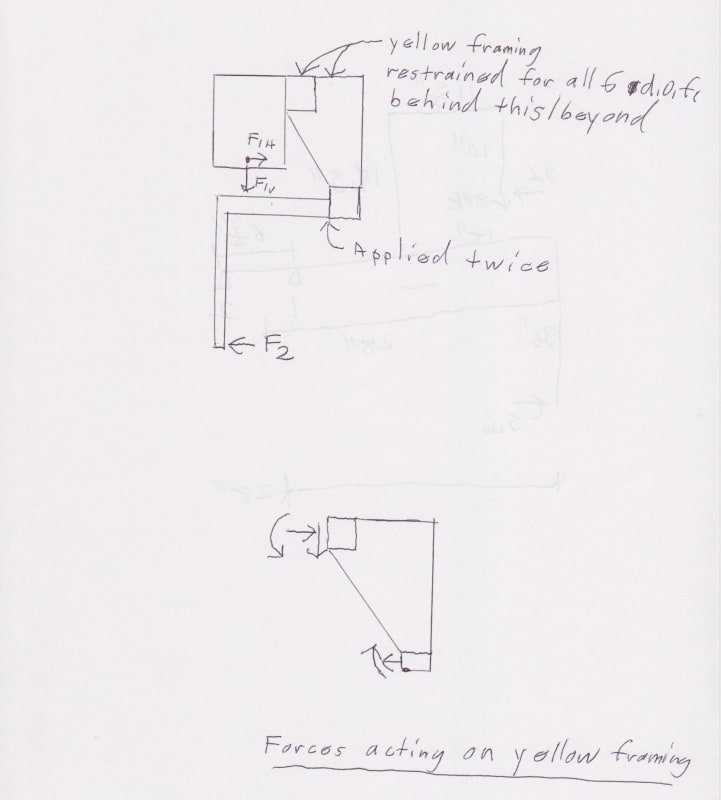
It is one of those brain freeze moments. I need some help with the statics for attached lifting beam fork analysis. Will the fork induce any torsion in the beam? It is supported at the bottom flange with wheels on ea side. How to resolve for forces in the setup. Thanks....