To all,
This actually hits on a topic that has been a question in my mind for a little while, and I am hoping to get someones opinion on it as it directly affects how I think about this topic. I may be way off base here and there may be some basic errors in how I set up my examples, but I do do believe my geometry and the basic premise is sounds.
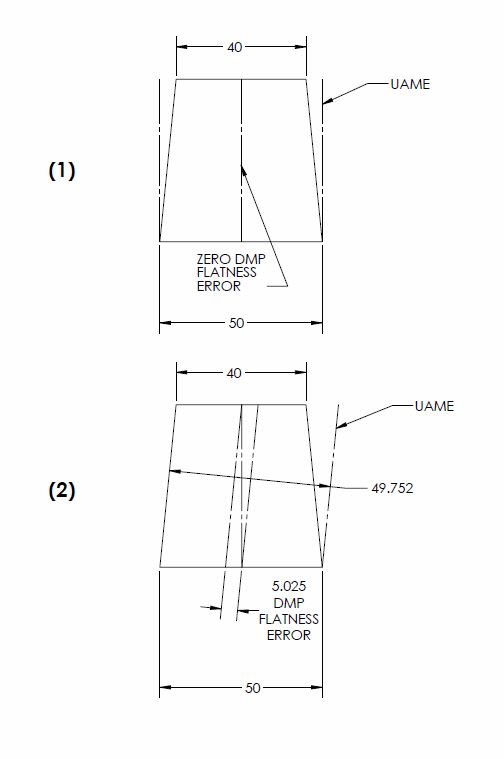
What do you guys think about the below figures? When a shape of "uniform symmetrical taper" is assessed in everyones above calculations, I believe you are assuming that the UAME looks something like #1 below which allows the parallelism error to be independent of any DMP flatness specification applied and only be a factor of the size tolerance (and therefore allowable taper). However, according to the definition of Actual Mating Envelope in Y14.5 section 1.3.25 "A similar perfect feature(s) counterpart of
smallest size that can be contracted about an external feature(s) or largest size that can be expanded within an internal feature(s)" - which would be the UAME I have shown in example #2, as you can see it is the smallest shape which can be fit around the feature. A UAME defined as my example #2 means that even a part with "uniform symmetrical taper" will still have measurable flatness error.
Of course I have increased the dimensions to show my point more clearly, and I know that the size of the UAME will approach the size of the maximum dimension as the difference between the toleranced dimension becomes smaller however it seems that even this very slight difference in the way the UAME is defined has significant effects on how DMP flatness is measured.
Utilizing the sizes in Figure 5-8 referenced by Kedu the UAME (per my above definition of UAME defined by my example #2) of a shape of uniform symmetrical taper (16 at one side 15.89 at the other) is 15.99999032.
This results in a maximum parallelism error that everyone has previously stated of ~0.11 (0.10999993 exact) however it results in a flatness error of ~0.055 (0.05500003 exact) which significantly violates the allowable flatness error of 0.04 - note my "exact" figures may differ from pmarc's due to slight rounding errors and how I set up my geometry. Note that the parallelism error is very nearly twice that allowed by DMP flatness, therefore if the UAME is to be defined in this manner I stand by my initial statement that the allowable parallelism is limited to 0.08