fa2070
Structural
- Jun 6, 2007
- 58
Hello,
Let's consider this situation.
I need to design a concrete slab-on-grade for a site with an ML-type soil. (sandy silt). The contractor is going to strip the upper layer of natural soil (1.00m thick) and replace it with sheepfoot-roller compacted structural fill (k > 300pci). The underlying strata are natural soil (-1.00m and beyond).
My question then is,
What modulus of subgrade reaction "k" do I have to use in my calculations to design this slab-on-grade? Should I use the "k" of the underlying natural silt or the "k" of the roller compacted fill (which ultimately will be supporting the slab) ?
Thanks.
Let's consider this situation.
I need to design a concrete slab-on-grade for a site with an ML-type soil. (sandy silt). The contractor is going to strip the upper layer of natural soil (1.00m thick) and replace it with sheepfoot-roller compacted structural fill (k > 300pci). The underlying strata are natural soil (-1.00m and beyond).
My question then is,
What modulus of subgrade reaction "k" do I have to use in my calculations to design this slab-on-grade? Should I use the "k" of the underlying natural silt or the "k" of the roller compacted fill (which ultimately will be supporting the slab) ?
Thanks.



![[cheers] [cheers] [cheers]](/data/assets/smilies/cheers.gif)
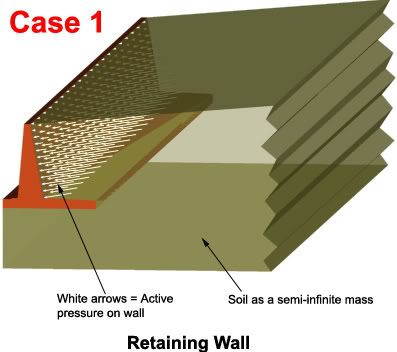
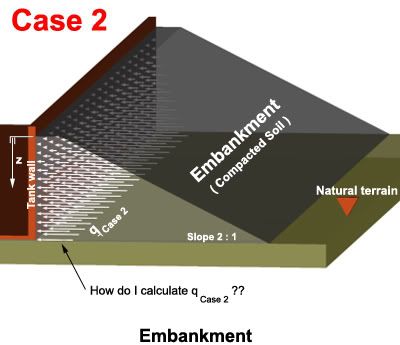
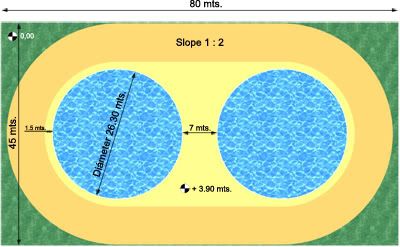
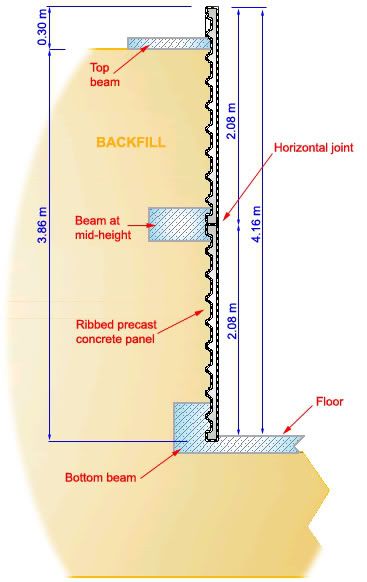



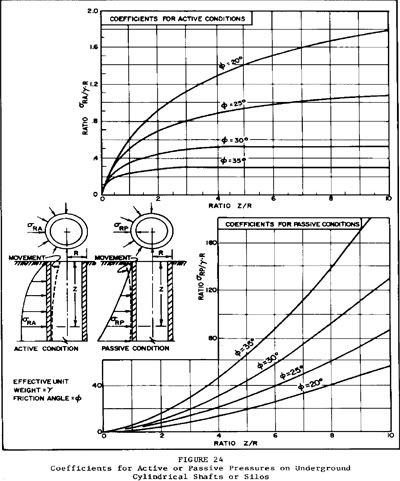

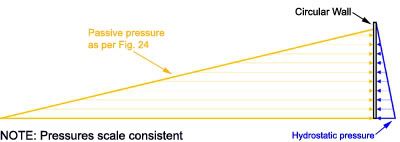
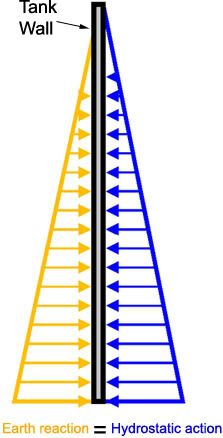
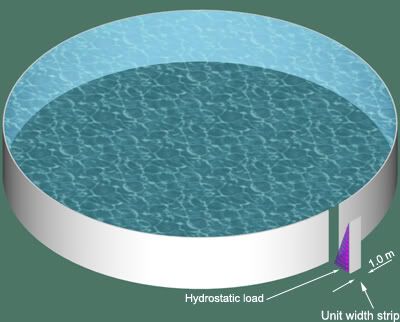

![[sad] [sad] [sad]](/data/assets/smilies/sad.gif)