I don't even know what this type of equation is really called, so I'm having difficulty even searching for a solution.
I wonder can anyone show a step by step solution to this, or is it purely a case of solving it by iteration?
sin(x) = sin(2x+s)+1
cos(x) = cos(2x+s)
Find x and s to satisfy the two above statements.
I do believe there are at least two solutions to this. (+ve s and -ve s)
(I suppose in this case there are infinite solutions after each period of sin x, since 2x is a direct multiple of x, but in reality if we suppose 2x was replaced by 1.9278x or some other random value, then the solution is no longer going to be every period of sin x).
The solution has a real life application, but I didn't want to include my application lest it just caused more confusion.
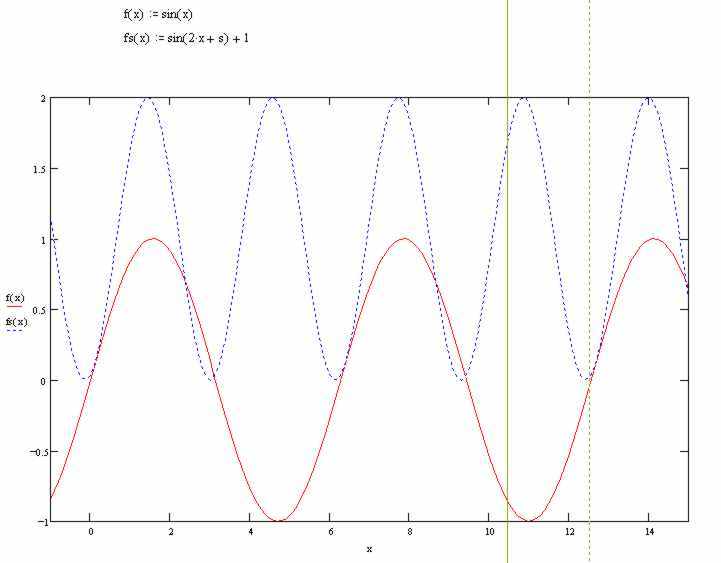
Below is an illustration of a graphically guessed solution. (guessed value of s=1.3)
I'm trying to solve where the two waves are tangential.
Thanks
I wonder can anyone show a step by step solution to this, or is it purely a case of solving it by iteration?
sin(x) = sin(2x+s)+1
cos(x) = cos(2x+s)
Find x and s to satisfy the two above statements.
I do believe there are at least two solutions to this. (+ve s and -ve s)
(I suppose in this case there are infinite solutions after each period of sin x, since 2x is a direct multiple of x, but in reality if we suppose 2x was replaced by 1.9278x or some other random value, then the solution is no longer going to be every period of sin x).
The solution has a real life application, but I didn't want to include my application lest it just caused more confusion.
Below is an illustration of a graphically guessed solution. (guessed value of s=1.3)
I'm trying to solve where the two waves are tangential.
Thanks

