bojoka4052
Mechanical
- Oct 8, 2021
- 108
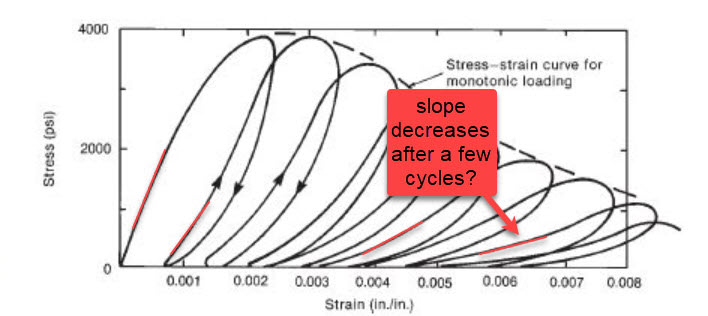
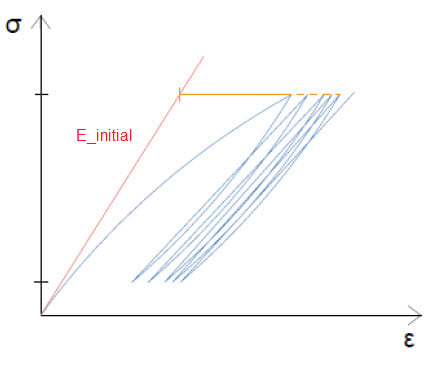
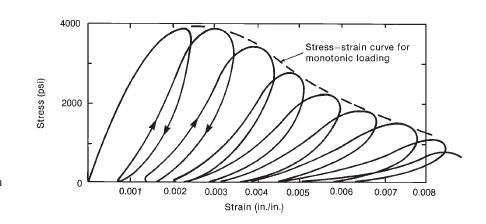
I have a concrete sample (preloaded), which has an initial Youngs Modulus (E). It is then loaded and unloaded several times. As you can see on the curve below the stress-strain relationship becomes nonlinear; should one not expect the Youngs modulus to be reduced? Reading previous notes it seems to think the youngs modulus increases the more times its loaded/unloaded.


![[pipe] [pipe] [pipe]](/data/assets/smilies/pipe.gif)