Sheet metal Spring, Force to Compress To a smaller Diameter 2

[Zibraz]

I'm struggling to determine the force to reduce this sheetmetal spring to Ø17.8mm.

If someone could point me in the direction or give advice, that would be great. I can find alot about normal wire springs, but can't find much for a sheetmetal spring. The spring is 0.6mm thick and 10mm long.

Thanks!

 

[MintJulep]

Force applied where?

Reacted where?

Why would you think it will stay a circular arc when deflected?

 

[Zibraz]

Force applied where?

Reacted where?

Why would you think it will stay a circular arc when deflected?

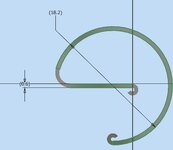
This sheetmetal spring is going to be inserted into a cylinder with a Ø17.80 bore. So the whole diameter will be compressed. I want to know how much force will be exerted outwards into the walls of the cylinder (Or know how much force it needs to compress the diameter.

 

[dvd]

Include thickness tolerance range in your analysis.

 

[GregLocock]

So imagine a radial , distributed , load on the green bit. The change in curvature is uniform along the beam so it is tempting to jump to the useful beam equation M/I=E/R. The only unknown is M, the derivative of that is the shear force which is the load in the first sentence. I doubt it is constant but could be wrong.

 

[CWB1]

I would search Machinery's Handbook and other texts for clock springs, and if all else fails try Google.

 

[3DDave]

Since it isn't uniformly loaded it won't be uniformly curved, but basically it is closing a curved beam by the difference in diameters. I don't have curved beam formulae at hand, but they are easy to find.

 

[Stress_Eng]

I found this problem quite interesting, so I gave it a go from first principals. I've assumed the forced displacement and included ''contact''. The results show only a few points are in contact, and the level of forces needed to make the clip take the desired shape is quite low. You'll probably decide to go for a different method, but the attachment may give you some ideas.

 

[desertfox]

Hi zibraz
Typically I would use Castigliano’s theorem to solve this problem however you need to identify points that will be fixed during compression because there is no way the spring of that shape will compress uniformly from the free diameter to the compressed diameter. You will end up with possibly two points of that spring reacting against the wall of the tube.
Using a spring in the shape of a circlip would be a much better starting point.
Finally it will only act as a spring if the stresses in the compressed shape do not exceed the yield stress for that spring material.
I have designed lots of different springs over my working life and just looking at that shape I doubt it will work the way you want it too.
Start off by setting the required forces of the spring and what you wish it to achieve for your device, then and only then can you set about calculating spring deflection, material etc.

 

[drawoh]

I'm struggling to determine the force to reduce this sheetmetal spring to Ø17.8mm.

If someone could point me in the direction or give advice, that would be great. I can find alot about normal wire springs, but can't find much for a sheetmetal spring. The spring is 0.6mm thick and 10mm long.

Thanks!View attachment 15692

You need to go back to basic beam analysis theory.

M = EI/R​

R is the bend radius over and above what you already have. I don't think you can solve this algebraicly, but you can do it numerically. Matlab or Octave are good, this is within the capabilities of Excel.

 

[3DDave]

from desertfox - a good point

Finally it will only act as a spring if the stresses in the compressed shape do not exceed the yield stress for that spring material.

But to add to that, it's not just the compressed shape, but that the item usually requires more compression than that to get it to fit, so there needs to be consideration for how much smaller the shape could be than the desired end result. Not that I would know anything about damaging small springs while trying to get them into place or anything like that.

 

[GregLocock]

While I wait for the carrier pigeon to deliver Stress_eng’s file I predict 3 points of contact at-90,45 and. +180 degrees, roughly, where 0 is up. That puzzles me, I thought rollpins were better than that

 

[3DDave]

Oh, shoot, I missed that this is a roll pin. As soft as this is I doubt that there will be line contact and will end up touching just 4-5 points.

 

[GregLocock]

Here’s how I think you solve it properly assuming no friction and symmetry about what I’ve called the 45 degree line. Apply a force pair at 45+/-theta. They are radial and of unit force. Calculate the reaction at 45 and the deflection at every point. Build up that matrix of deflections,assign a weighting to each row and the sum of weighting*deflection for each column.Then use an optimiser to adjust the weightings to meet the 0.02 at each theta.