I have this 4m cantilever flat slab that has 35mm long term deflection using normal non-PT RC slab analysis. I just wanna know if there is any way that I can estimate the deflection of a PT one based on the normal RC model that I have built? (doesn't need to be accurate, just wanna know how much deflection roughly PT can save). I am not familiar with PT slab and it will be designed by others. Right now I just wanna estimate the thickness without establishing a detailed model with tendons in so I can keep going with my structure. Thank you.
Tek-Tips is the largest IT community on the Internet today!
Members share and learn making Tek-Tips Forums the best source of peer-reviewed technical information on the Internet!
-
Congratulations MintJulep on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
Rule of thumb for PT slab deflection?
- Thread starter dis_
- Start date
How did you determine your RC slab long-term deflection magnitude of 35mm - cracked section, with accurate estimate of creep and shrinkage deflections?
For a given span, with PT design you have two significant variables that the designer can use - structural depth (eccentricity) and prestress force. If you are trying to reduce 35mm of tip deflection for a 4m cantilever (Δ/L = 1/230) you may be able to reduce the slab depth for a given prestress force and eccentricity. In theory you could make the cantilever tip deflection zero with a PT solution, but that will not be practical assuming building-type loadings, facade loads, economics, etc.
With you existing RC model, you could apply EQUIVALENT LOADS due to prestress (due to tendon curvature, eccentricity and change of CG) as a load case (making an allowance for prestress losses), and add that load case to your serviceability load cases. It may give you an indication of deflections - but it depends on the severity/magnitude of flexural stresses. Based upon the chosen level of prestress you would need to manually check flexural strength at critical sections etc. Not a particularly elegant solution.
I am old-school - so what we did before computers to get a trial section - I would do a few hand calcs and determine an appropriate D and Pef using equivalent loads. First check punching shear to arrive at a starting depth based upon say 1.5 MPa of P/A - be careful of P/A at corner and edge columns. Start with balancing say 75% of SW, this will get you your tendon eccentricities, calc your equivalent loads, then do a quick moment distribution, check flexural stresses at peak M- and M+, check elastic-calc deflections, see what the magnitude is, allow for approx time-dependent effects, then adjust prestress and/or depth, as required.
For a given span, with PT design you have two significant variables that the designer can use - structural depth (eccentricity) and prestress force. If you are trying to reduce 35mm of tip deflection for a 4m cantilever (Δ/L = 1/230) you may be able to reduce the slab depth for a given prestress force and eccentricity. In theory you could make the cantilever tip deflection zero with a PT solution, but that will not be practical assuming building-type loadings, facade loads, economics, etc.
With you existing RC model, you could apply EQUIVALENT LOADS due to prestress (due to tendon curvature, eccentricity and change of CG) as a load case (making an allowance for prestress losses), and add that load case to your serviceability load cases. It may give you an indication of deflections - but it depends on the severity/magnitude of flexural stresses. Based upon the chosen level of prestress you would need to manually check flexural strength at critical sections etc. Not a particularly elegant solution.
I am old-school - so what we did before computers to get a trial section - I would do a few hand calcs and determine an appropriate D and Pef using equivalent loads. First check punching shear to arrive at a starting depth based upon say 1.5 MPa of P/A - be careful of P/A at corner and edge columns. Start with balancing say 75% of SW, this will get you your tendon eccentricities, calc your equivalent loads, then do a quick moment distribution, check flexural stresses at peak M- and M+, check elastic-calc deflections, see what the magnitude is, allow for approx time-dependent effects, then adjust prestress and/or depth, as required.
- Thread starter
- #3
Thanks for your detailed explanation.
The RC slab was performed using FEA with consideration given to cracking, creep (coefficient=2) and shrinkage (0.0004 strain). I am trying to reduce the slab thickness a bit (to 250mm if possible) and deflection to within L/125 limit.
Punching shear has been checked in my model and I don't think PT will affect this much?
I have very little knowledge about PT and as I said, it will be designed by other contractor. At this stage I just wanna know if there is any "quick" way to know how much deflection PT can save roughly.
The RC slab was performed using FEA with consideration given to cracking, creep (coefficient=2) and shrinkage (0.0004 strain). I am trying to reduce the slab thickness a bit (to 250mm if possible) and deflection to within L/125 limit.
Punching shear has been checked in my model and I don't think PT will affect this much?
I have very little knowledge about PT and as I said, it will be designed by other contractor. At this stage I just wanna know if there is any "quick" way to know how much deflection PT can save roughly.
This might be as good as approach as any for your purposes. It's not for cantilevers but I'd think that you could ratio your deflections in the same way +/-. Obviously, the real answer depends on a bunch of complicated stuff. This is based on unbonded systems common in North America.
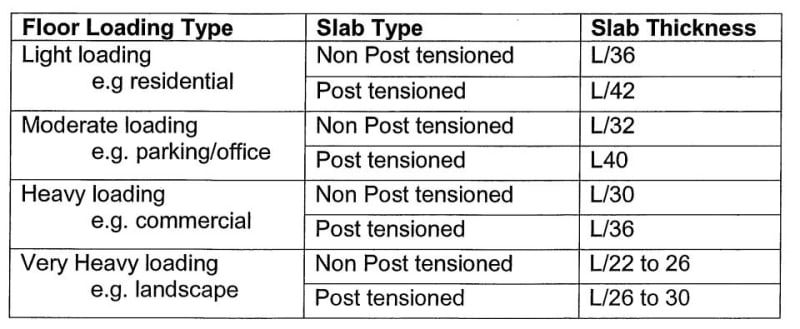
- Thread starter
- #6
Thank you Kootk and rapt.
Rapt,
I understand that there is no rule of thumb for deflection for RC or PT cantilever slab deflection. But what I am asking here is based on the deflection that I get from the RC model I built is there any way to estimate the deflection when tendons are used?
Rapt,
I understand that there is no rule of thumb for deflection for RC or PT cantilever slab deflection. But what I am asking here is based on the deflection that I get from the RC model I built is there any way to estimate the deflection when tendons are used?
You have two ways to estimate the PT slab thickness:
1) Familiarize with the general concept of how PT works, and how PT controls strength level and deflection.
2) Work with your PT partner.
The final deflection needs to satisfy the service criteria/needs.
1) Familiarize with the general concept of how PT works, and how PT controls strength level and deflection.
2) Work with your PT partner.
The final deflection needs to satisfy the service criteria/needs.
dis said:
Some thoughts:
1) The low hanging fruit is Ingenuity's suggestion of applying the PT balancing load as an upwards load to your model (downwards in the back span). That should make a pretty good improvement in your dead load deflections.
2) If your concern is service load deflection, you might run some quick numbers to see if a reasonable level of prestress would prevent your slab from cracking over the support at the peak moment location. If that's the case, then you can consider something closer to the gross moment of inertia for your slab stiffness as apposed to a cracked moment of inertia.
3) For a given slab depth, I would expect a PT slab to exhibit less creep deformation than a mildly reinforced slab. That said, I don't know how to quantify this readily and it may not be true in all situations. Also, if the PT slab would be thinner than the non-PT slab, that kind of ruins this argument.
- Thread starter
- #9
- Status
Similar threads
- Locked
- Question
