human909 said:
Your statement seems to mistinterpret the code and is a little bit recursive if you determine the critical flange in the context of existing restraints. Could you possibly elaborate? Am I just misinterpretting your statement. Thanks in advance.
I believe that the confusion has come about because the Aussi-clause below is
also in serious need of an overhaul. More so, actually, than even the "compression flange" business because this clause will be egregiously misleading, in a theoretical sense, 100% of the time. That it will often lead designers to make the right choice anyhow is little more than coincidence.
AS4100 said:
The critical flange at any cross-section is the flange which in the absence of any restraint at that section would deflect the farther during buckling.
I've been reticent to get into this part of things because it requires going deep,
deep into the theoretical weeds of the stability swamp. Now that you've asked the question, however, it's time.
1) As designers, we tend to think that there exist a handful of buckling possibilities for any particular member and that, once those have been checked, buckling is no longer possible. This is true in a practical/functional sense but is not true in a theoretical sense. Theoretically, there are an infinite number of possible buckling modes. Like a buckling multi-verse of sorts.
2) Each possible buckling mode is associated with a particular strain energy that is required for the member to assume the proposed buckled shape. What we mean by "critical buckling mode", is the next buckling mode in the infinite series that would be associated with the lowest strain energy. As in all things, nature strives to minimize energy.
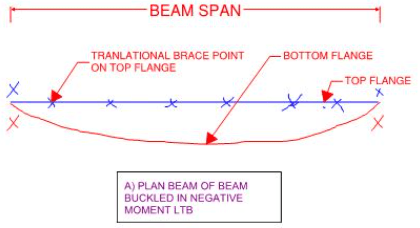
This is complicated by the fact that the intervals between different buckling modes is not uniform. The 902 nd buckling mode might require 20X the strain energy of the 901 st buckling mode. But, then, the 903 rd buckling mode might require only 1.05X the strain energy of the 902 nd buckling mode. This is why I use the dual path, bifurcated checking approach that I mentioned previously for beams with inflection points. For such beams, I can't tell by inspection whether positive bending LTB or negative bending LTB governs. So I check both. And I pray to the powers that be that the 904 th buckling mode is miles off in the distance as far as strain energy goes.
3) For the purpose of this discussion, the important takeaway of #2 is that all buckling checks must start with the designer
assuming a critical buckling mode. Not knowing...
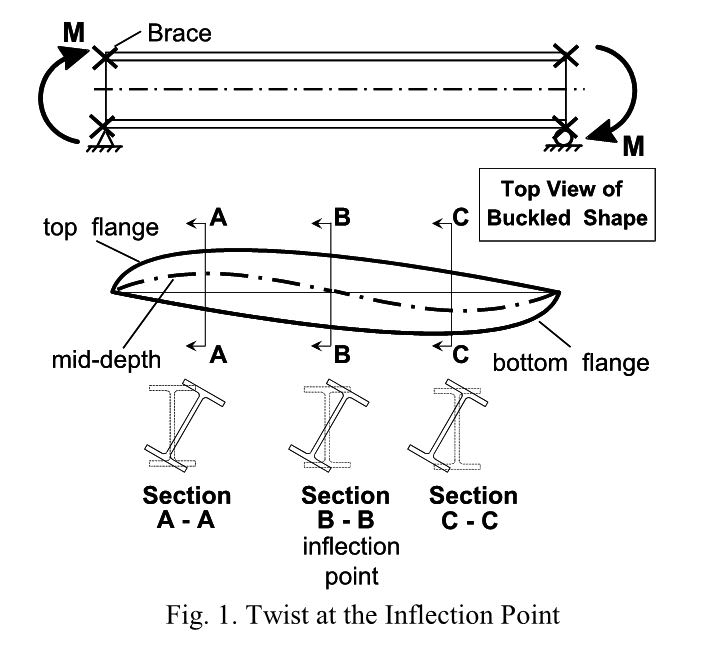
assuming (hopefully based on good judgement). This is what I did with the sketch below, taken from the beginning of this thread.
4) The assumed buckling mode shape from #3 must pay homage to the physical restraints that form the boundary conditions of the problem (lateral top flange braces here). Otherwise, we're no longer discussing an LTB mode shape that has any bearing on our real world situation. Again, this is what I did with the sketch below, taken from the beginning of this thread.
5) In the AS4100 procedure, they
end with finding the assumed LTB mode shape (critical flange) rather than starting with it. And, in my opinion, this is a serious mistake and is what leads to things having a recursive, chicken and egg feel to them. There's just nothing meaningful to check in the world of LTB until AFTER an LTB buckling mode shape has been assumed.
6) The AS4100 business about the "absence of any restraint" seems to lead designers to examining a case where all restraints are removed as a means of establishing the LTB buckling shape for a case
when all of the physical restraints are present. How much sense does that make? None. And, in spite of the way that the provision is written, I'm sure that it's not what anyone actually intended.
7) The AS4100 provision could be revised, quite easily, as follows:
a) The critical flange at any cross-section segment is the flange which in the absence of any restraint at that section would deflect the farther during buckling given the lateral and torsional restraints present. OR;
b) The critical flange at any cross-section segment is the flange which, in the absence of any additional restraint at that section contemplated by the designer would deflect the farther during buckling. given the lateral and torsional restraints present.
Modest changes but enormous implications. It's minor but we also shouldn't be speaking in terms of "cross sections". Rather, we should be speaking in terms of "segments" because LTB is a linear phenomenon rather than a point phenomenon.