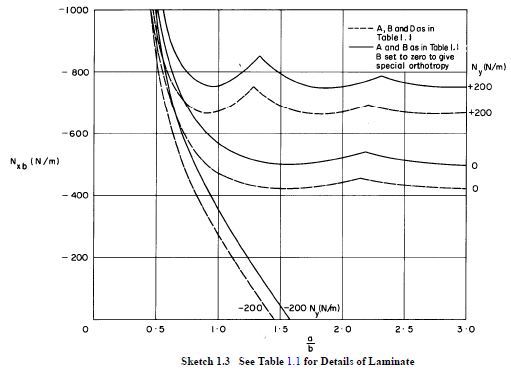
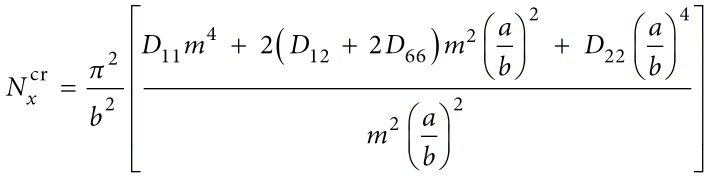For an isotropic material with a unaxial stress (or running load), the function of the chart is to pair the coefficient with the stability equation Fcr=(Pi^2*Kc*Ec*(t/b)^2)/(12(1-v^2)). This can be done for various edge conditions, but that chart is for all edges simply supported. An isotropic material has 2 independent elastic constants, which are part of the equation.
On the other hand, a composite laminate has at least 4 independent elastic constants that affect the stability solution (D11, D22, D12, D66). This is assuming the laminate is balanced, that bend-twist coupling is minor, and that the transverse shear stiffness does not affect the solution. In the event that the laminate is unsymmetric, the D* components are preferred.
So rather than use a chart that gives you a coefficient, you can solve for the following equation for composites. The simple case for uniaxial loading and all edges simply supported is in MIL-HDBK-17, CMH-17, and various other publications. If you were to solve this equation for an isotropic material, you would see that you will be able to back out the Kc values and they are identical to the chart you attached. That is actually how the charts are developed (backing out coefficients from the analytical solutions - if available).
Brian