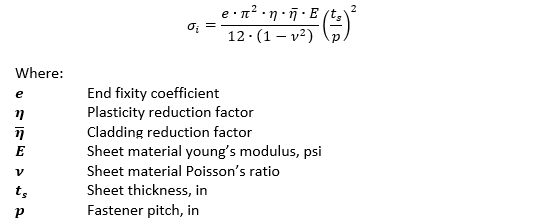I have all the books you mentioned above, what is Alteon I don't know, Please give me full reference.
Alteon was a company that did structural analysis training for engineers and was acquired by Boeing. So it's a Boeing company but they have a lot of training slides/notes out there that are not proprietary material.
Please show one of your calculations and How to calculate F0.7.
In this case I just did it graphically. Use the stress-strain curve, draw a line that's 0.7E and find where it intersects with the curve. Alternatively you can do this mathematically if you have the Ramber-Osgood K and n values or Hollomon parameters for the material.
I'm still a bit confused though, since your applied compressive stress is in excess of both the interfastener buckling strength and the material Fcy.
Of course we don't always consider buckling to be a failure, in most situations a section can be loaded well in excess of buckling before failure. And of course there are plastic buckling methodologies that can be implemented in analysis. But those are primarily for situations where it's possible that the stress at initial buckling is above the yield strength of the material.
I understand we're talking about flat plates between fasteners here, but as a simple analogy let's just consider column buckling (plates & thin-walled structures are essentially the same, just with some tweaks to the methods). You can separate the load vs. L'/rho curve into regimes... for short slenderness ratio you'll either be block compression or crippling critical. Intermediate columns would fail in a complex mix of primary and secondary instability and you'd be using the Johnson-Euler method. For long columns, you'd basically just have primary instability and Euler or Euler-Engesser (if you want to account for plasticity) should be used. In order for the buckling strength to be over Fcy you'd either need a stiffened and supported assembly or a very short slenderness ratio. In that case you'd likely be crippling critical. But I suppose it's possible that since the crippling stress is defined as the average stress at failure, it's possible to have a buckling mode at a stress over Fcy, before crippling of the section occurs. In which case you'd need a plastic buckling method. Johnson-Euler is generally cutoff at Fcy. I guess it's also possible that you could be an intermediate column and want to take advantage of post-buckled strength in your design. So you want to know what happens if you keep loading past the interfastener buckling strength.
But your analysis shows you will elastically buckle first, and then your applied load keeps going all the way well past yield. So in order to show this structure is OK you need to take advantage of post-buckled strength and also show whatever permanent deformation occurs in the buckled state is non-detrimental? Seems like a tall order. I guess I'm still wondering what is being done here and why you're so set on showing this is OK. Seems to me like the design is insufficient.