I'm working in a reduction system and would like some help to be sure this is going to work properly.
The electric motor (green) is rated to 1.4HP @ 7500 RPM and the shaft torque = 187 in oz. The belt reduction is 2:1 and the planetary system info is
Rated Output Torque (in-lbs):177
Max Output Torque (in-lbs):283
Ratio:32:1
I'm trying to make a mid drive electric system for a bicycle and my concern is if the planetary reduction is strong enough.
Any advice would be welcome.
Thanks
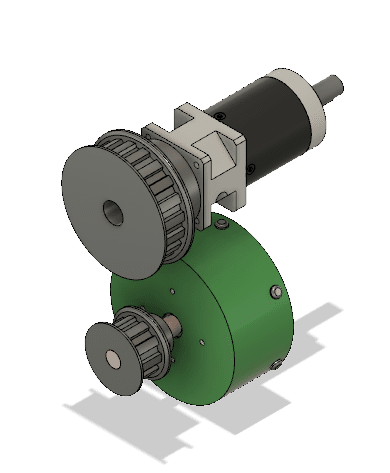
The electric motor (green) is rated to 1.4HP @ 7500 RPM and the shaft torque = 187 in oz. The belt reduction is 2:1 and the planetary system info is
Rated Output Torque (in-lbs):177
Max Output Torque (in-lbs):283
Ratio:32:1
I'm trying to make a mid drive electric system for a bicycle and my concern is if the planetary reduction is strong enough.
Any advice would be welcome.
Thanks




![[sad] [sad] [sad]](/data/assets/smilies/sad.gif)