Overturning Load Anchor Bolt Hand Calcs 4

[jStadts]

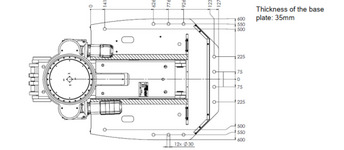
I have a project where overturning is a concern and am confused on how to get the "actual" tension in the anchor bolts that are being proposed. I understand the work flow through ACI on how to solve for the required strengths on concrete breakout and side face blowout etc. A lot of resources are based on a column baseplate with an even pattern of anchors and a centralized moment but my moment is from overturning where it is located at the left end of the baseplate. How do I go about solving for the actual tension on the bolts? The more specific issue is how would I solve for the minimum amount of anchors required to hold the machine down safely.

I've used Hilti Profis to get a general idea but I want to be able to verify via hand calcs.

 

[JAE]

If you have a circular pattern of bolts, the derivation of the bolt group moment of inertia is the SUM(Ad^2) where A is the individual bolt diameter and d is the distance from the bolt center to the neutral axis. Add up all these Ad^2 values for the bolts and you have a rough value of Ix for the group.

The bolt group area is the summation of the individual bolt areas of course.

Then take your axial load on the bolt group and the applied moment and use:
P/A +/- My/I to derive the maximum stress at the outer bolts where "y" is the distance to the center of the outer bolt.

This gets you a stress on that outer bolt and by multiplying it by the bolt area gets you the load on the bolt.

There will be, of course, several load combinations to check.

 

[jStadts]

If you have a circular pattern of bolts, the derivation of the bolt group moment of inertia is the SUM(Ad^2) where A is the individual bolt diameter and d is the distance from the bolt center to the neutral axis. Add up all these Ad^2 values for the bolts and you have a rough value of Ix for the group.

The bolt group area is the summation of the individual bolt areas of course.

Then take your axial load on the bolt group and the applied moment and use:
P/A +/- My/I to derive the maximum stress at the outer bolts where "y" is the distance to the center of the outer bolt.

This gets you a stress on that outer bolt and by multiplying it by the bolt area gets you the load on the bolt.

There will be, of course, several load combinations to check.

Wouldn't P/A be kN/m^2 and then My/l be kN/m?

P= 49.5kN
A= 1.53m^2

M= 56kNm
y= 1.25m
l= .31 m^3

Obviously don't need you to run through the numbers but just using units I'm still a little confused. Is it A*(d^2) or (A*d)^2? I guess the latter would work out unit wise.

 

[jStadts]

I guess in addition that that, I took the neutral axis at the left edge of the plate. Is that correct? Or is there something I have to do to move the moment from the left edge to the center of the plate?

 

[RWW0002]

You might check your units on your moment of inertia term

 

[JAE]

I = value in m^4

 

[jhnblgr]

https://www.towernx.com/downloads/Technical_Manual_MP_BasePL.pdf

This gives some examples

 

[HTURKAK]

JStadts;​

Apparently this a robotic arm supported on RC pedestal. If the base plate supported on levelling, compression nuts , the assumption that the developing forces tension and compression will be resisted by anchors is correct . In this case , you can calculate the moment of inertia of anchor points then find the anchor loads.
However, if the base plate is grouted , then post installed anchors applied or there is no compression nuts , the anchors will resist only to tension forces and compression force is resisted by base plate .
The reasonable approach would be ,assuming thick plate ( 35 mm thick is more than OK ) bending theory is valid , the neutral axis shall be located ( with trial and error for hand calc.) then calculate the anchor tension forces.

jhnblgr provided a great document (.https://www.towernx.com/downloads/Technical_Manual_MP_BasePL.pdf) .​

You can look also AISC Steel Design Guide DG-1 column base plates. ( seems free document at web )

 

[Stress_Eng]

Knowing the loading, I would construct a FBD for each load case. This will enable you to determine the load paths. For instance, it looks like that, before any bolt sees a tension load, the load has to migrate through the plate and go towards the outer edges. Would the bolts see a compression load, or is there an alternative stiffer load path that goes straight through the plate (e.g. through a vertical web and into ground)? I would determine your load paths first, then conduct a couple of BGA's, for each load case. If the bolts are the only load path to react tensile and compression, then your BGA may look something like the attached.

 

[HDStructural]

I typically have A as the area of the anchor bolt, not the diameter and it should be A * (d^2). However, if the anchor bolts are all the same size, I prefer to just use 1 for area that way we end up solving for a force in each bolt, rather than a stress in each bolt.

JAE wasn't using a true area of the bolts (and there is nothing wrong with that), he was just using the diameter, so P/A would be kN/m just as My/I is kN/m. Units are important with this and can get a bit complicated depending on how you treat the A in the equation.

 

[Stress_Eng]

This is a BGA using the info in your post. The calc's haven't been checked but it may give you some ideas.